The efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_236_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs". _E01_236_Q02.png)
A carnot engine whose low temperature reservoir is at 7∘C has an efficiency of 50%. It is desired to increase the efficiency to 70%. By how many degrees should the temperature of the high temperature reservoir be increased?Solution in Gujrati
273K
11203K
140K
None of these
The correct Answer is:B
η=T1−T2T1=0.5⇒T1=560K
η'=0.7=T'1−T2T'1=T'1−280T'1⇒28003
⇒T'1−T1=11203
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
48 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
40 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Two rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
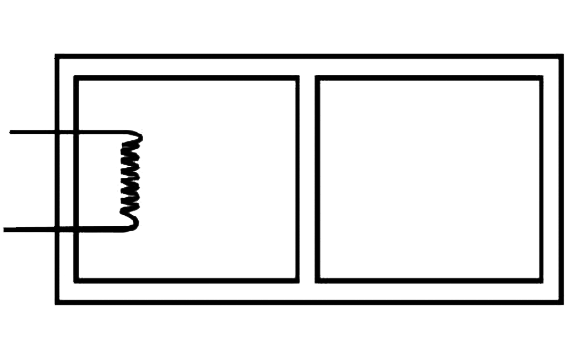
View SolutionThe rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas (λ=5/3) at a pressure P0, volume V0 and temperature T0. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes 243P0/32. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.
View SolutionStatement-1: A real gas behaves as an ideal gas at high temperature and low pressure .
Statement-2: Liquid state of an ideal gas is impossible.
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
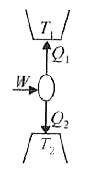
View SolutionConsider a heat engine as shown in (figure). Q_(1) and Q_(2) are heat added to heat bath T_(1) and heat taken from T_(2) one cycle of engine. W is the mechanical work done on the engine. If Wgt0 , then possibillities are:
View SolutionA heat engine absorbs heat Q_(1) at temperature T_(1) and Q_(2) at temperature T_(2) . Work done by the engine is (Q_(1)+Q_(1)) . This data:
View SolutionThe efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . eta = (W)/(Q_(1)) = (Q_(1) - Q_(2))/(Q_(1)) Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression. For carnot cycle (Q_(1))/(T_(1)) = (Q_(2))/(T_(2)) . Thus eta = (Q_(1) - Q_(2))/(Q_(1)) = (T_(1) - T_(2))/(T_(1)) According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs". An inventor claims to have developed an engine working between 600K and 300K capable of having an efficiency of 52% , then -
View SolutionThe efficiency of a heat engine is defined as the ratio of the mechanical work done by the engine in one cycle to the heat absorbed from the high temperature source . η=WQ1=Q1−Q2Q1 Cornot devised an ideal engine which is based on a reversible cycle of four operations in succession: isothermal expansion , adiabatic expansion. isothermal compression and adiabatic compression.
_E01_238_Q01.png)
For carnot cycle Q1T1=Q2T2. Thus η=Q1−Q2Q1=T1−T2T1 According to carnot theorem "No irreversible engine can have efficiency greater than carnot reversible engine working between same hot and cold reservoirs"._E01_238_Q02.png)
Efficiency of a carnot's cycle change from 16 to 13 when source temperature is raised by 100K. The temperature of the sink is-
View SolutionA heat engine absorbs heat Q_(1) at temperature T_(1) and heat Q_(2) at temperature T_(2) . Work done by the engine is (Q_(1)+Q_(2)) . This data
View SolutionA heat engine absorbs heat Q1 at temperature T1 and heat Q2 at temperature T2, work done by the engine is J (Q1+Q2) this data
View SolutionA heat engine absorbs heat q1 from a source at temperature T1 and heat q2 from a source at temperature T2. Work done is found to be J(q1+q2). This is in accordance with
View Solutionएक ऊष्मा इंजन एक स्रोत से ताप T1 पर q1 ऊष्मा अवशोषित करता है तथा एक अन्य स्रोत से तापा T2 पर q2 ऊष्मा अवशोषित करता है। किया गया कार्य (q1+q2)J पाया जाता है। यह किस नियम के अनुसार होता है?
View SolutionConsider a heat engine as shown in figure. Q_(1)and Q_(2) are heat added both to T_(1) and heat taken from T_(2) in one cycle of engine. W is the mechanical work done on the engine. If Wgt0 , then possibilities are
View SolutionConsider a heat engine as shown in (figure). Q_(1) and Q_(2) are heat added to heat bath T_(1) and heat taken from T_(2) one cycle of engine. W is the mechanical work done on the engine. If Wgt0 , then possibillities are:
View Solutionचित्रानुसार कोई ऊष्मा इंजन है। Q1 एवं Q2, ऊष्मा भण्डार T1 को दी जाने वाली तथा इंजन के एक चक्र में T2 से ली जाने वाली ऊष्मा हैं। W इंजन पर किया गया यांत्रिक कार्य है। यदि W>0, तो संभावनाएँ हैं-
(i) Q1>Q2>0 (ii) Q2>Q1>0
(iii) Q2<Q1<0 (iv) Q1<0,Q2>0
View Solution
