A Carnot engine takes 3×106 cal of heat from a reservoir at 627∘C and gives it to a sink at 27∘C. The work done by the engine is:Solution in Gujrati
(a)4.2×106J
(b)8.4×106J
(c)16.8×106J
(d)zero
The correct Answer is:B
Tsource=627∘C=627+273=900K
Tsink=27∘C=27+273=300K
Efficiency (η)=1−TsinkTsource=1−300900=1−13
(η)=23=OutputInput=WorkHeatInput
⇒23×Heat Input=Work
⇒23×3×106×4.2=Work
⇒Work=8.4×106J
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B)
58 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B) (MCQ)
9 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300K. The ratio of the average rorational kinetic energy per O2 molecules to that per N2 molecules is
View SolutionLet ¯v,vrms and vp respectively denote the mean speed, the root-mean - square speed, and the most probable speed of the molecules in an ideal monoatomic gas at absolute temperature T. The mass of a molecule is m:-
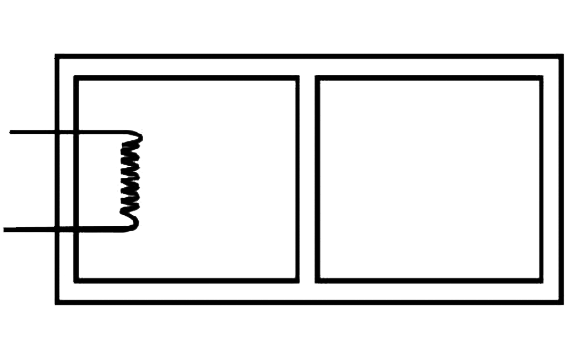
View SolutionThe rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas (λ=5/3) at a pressure P0, volume V0 and temperature T0. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes 243P0/32. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA Carnot engine takes 3×106 cal of heat from a reservoir at 627∘C and gives it to a sink at 27∘C. The work done by the engine is:
View SolutionA carnot engine takes 6000 cal of heat from a reservoir at 627^(@)C and gives it to a sink at 27^(@)C . The work done by the engine is
View SolutionA heat engine takes in 300 K cal of heat from a reservoir at 627^(@)C and gives it to a sink at 27^(@)C . The work done by the engine is
View SolutionA Carnot engine takes 3 × 106 cal of heat from a reservoir at 627°C, and gives to a sink at 27°C. The work done by the engine is
View SolutionA carnot engine takes in 3000 kcal of heat from a reservoir at 627^@C and gives a part of it to a sink at 27^@C . The work done by the engine is
View SolutionA Carnot engine takes 9000 cal of heat from a reservoir at 627^@ C and gives it to a sink at 27^@C . The work done by the angine is
View SolutionA Carnot engine takes 3 xx 10^(6) cals of heat from a reservoir at 627^(@)C and gives it to a sink at 27^(@)C . The work done by the engine is:
View SolutionA carnot engine takes in 3000 kcal of heat from a reservoir at 627°C and gives it to a sink at 27°C. The work done by the engine is
View SolutionA Carnot engine takes 3×106 cal of heat from a reservoir at 627∘C and gives it to a sink 27∘C. The work done by the engine is
View SolutionA Carnot engine takes 3×106 cal of heat from a reservoir at 627∘C and gives it to a sink at 27∘C. The work done by the engine is:
View SolutionA Carnot engine takes 3×106 cal of heat from a reservoir at 627∘C and gives it to sink at 27∘C. What is the work done by. the engine ?
View Solution
