Two protons are having same kinetic energy. One proton enters a uniform magnetic field at right angles ot it. Second proton enters a uniform electric field in the direction of field. After some time their de Broglie wavelengths are λ1andλ2 then
(a) λ1=λ2
(b) λ1<λ2
(c) λ1>λ2
(d) some more information is required Solution in Gujrati
The correct Answer is:D
We have work is done by only electric field. Thus if ¯¯¯E||→v,|→v| decreases, & thus momentum of electron decreases & vice-versa, while in magnetic field |→v| remains constant.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 35
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 36
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise - 33
2 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
An electron with initial kinetic energy of 100eV is acclerated through a potential difference of 50V. Now the de-Brogile wavelength of electron becomes
View SolutionWhen a photon of light collides with a metal surface, number of electrons, (If any) coming out is
View Solution10−3 W of 5000A light is directed on a photoelectric cell. If the current in the cell is 0.16μA, the percentage of incident photons which produce photoelectrons, is
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionIf the two roots of the equation (λ−2)(x2+x+1)2−(λ+2)(x4+x2+1) are real and equal for λ=λ1,λ2 then λ1+λ2=0 (b) |λ1−λ2|=6 (c) λ1+λ2=32 (d) all of these
View SolutionThe energy of a photon is equal to the kinetic energy of a proton. The energy of the photon is E. Let lambda_1 be the de-Broglie wavelength of the proton and lambda_2 be the wavelength of the photon. The ratio (lambda_1)/(lambda_2) is proportional to (a) E^0 (b) E^(1//2) (c ) E^(-1) (d) E^(-2)
View SolutionTwo protons are having same kinetic energy. One proton enters a uniform magnetic field at right angles ot it. Second proton enters a uniform electric field in the direction of field. After some time their de Broglie wavelengths are lambda_1 and lambda_2 then (a) lambda_1 = lambda_2 (b) lambda_1 lt lambda_2 (c) lambda_1 gt lambda_2 (d) some more information is required
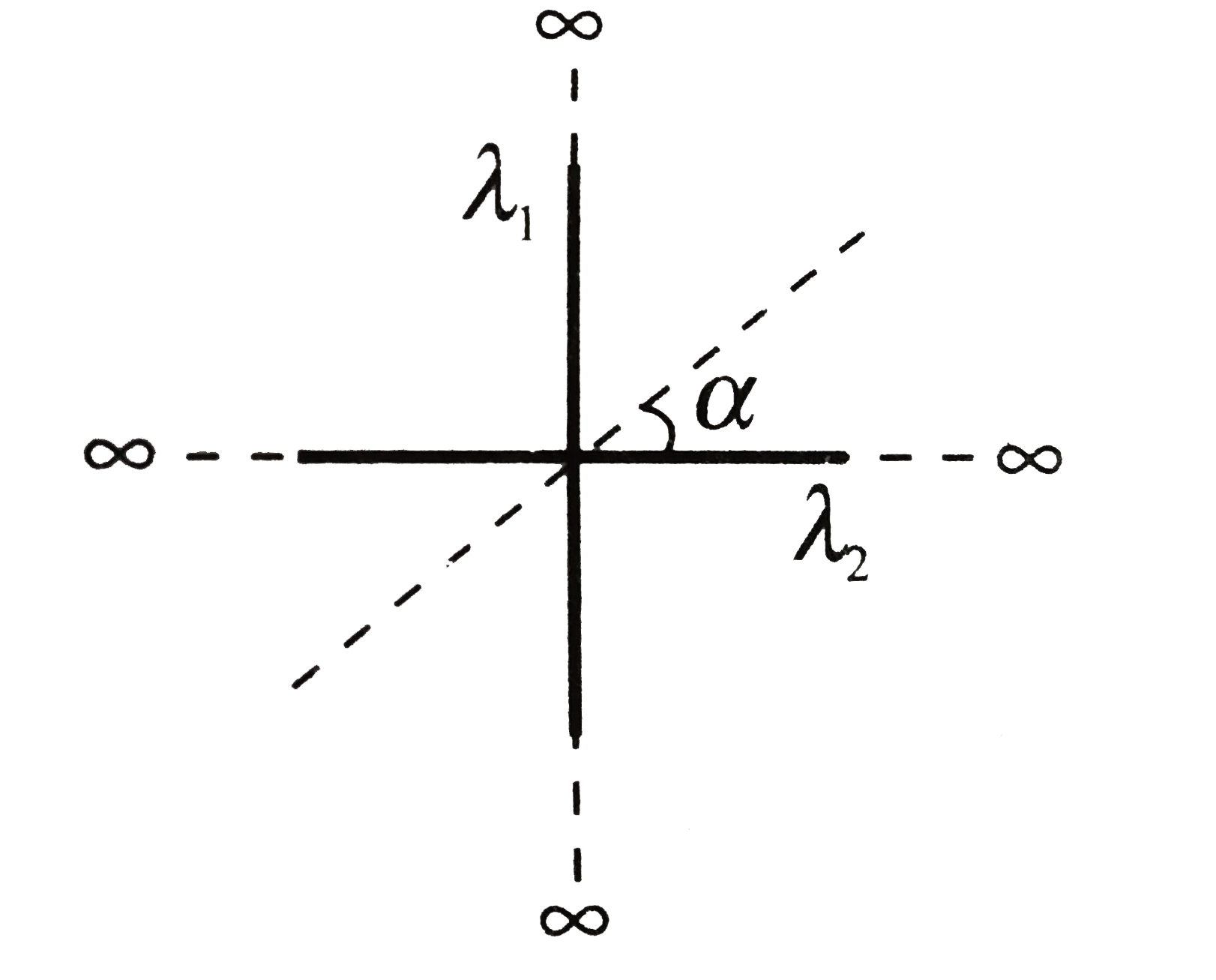
View SolutionTwo mutually perpendicular wire carry charge densities λ1andλ2. The electric lines of force makes angle α with second wire, then λ1/λ2 is
View Solutionthe energy of photon is equal to the kinetic energy of a porton,If lambda_1 is the De-Broglie wavelength of a proton, lambda_2 the wavelength associated with the proton and if the energt of the protonis E, then (lamda_1//lambda_2) is proportional to
View SolutionA source emitting light of wavelengths λ1andλ2 is used in Young's double-slit experiment. If fourth bright of λ1 coincides with sixth bright of λ2, then
View SolutionIf lambda_1,lambda_2 and lambda_3 The origin of closed argon tube waves are the resonant wavelength of the first and second hypersensitivity, then the ratio lambda_1:lambda_2:lambda_3 Will happen
View SolutionIf λ1andλ2 , are the wavelengths of the third member of Lyman and first member of the Paschen series respectively, then the value of λ1:λ2 is:
View Solutionλ1 तरंगदैर्ध्य के प्रकाश से उत्सर्जित फोटो इलेक्ट्रान की अधिकतम गतिज उर्जा K1 एवं λ2 के लिये K2 है। यदि λ1=2λ2 हो तब
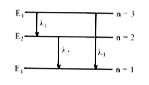
View Solutionएक परमाणु के तीन ऊर्जा स्तर चित्र में दिखाये गये है। तीन सम्भव विकरण से सम्बन्धित तरंगदैर्ध्य lambda_1, lambda_2" और "lambda_3 का मान λ1 और λ2 के पदों में दिया जा सकता है।__________
View SolutionThe energy of a photon is equal to the kinetic energy of a proton. The energy of the photon is E. Let lambda_1 be the de-Broglie wavelength of the proton and lambda_2 be the wavelength of the photon. The ratio (lambda_1)/(lambda_2) is proportional to (a) E^0 (b) E^(1//2) (c ) E^(-1) (d) E^(-2)
View Solution
