A particle moves along a straight line and its position as a function of time is given by x=t6(3)−3t6(2)+3t+3, then particle Solution in Gujrati
stops at t−1s and reverses its direction of motion
stops at 1-1s and continues further without change of direction
stops at 1-2s and reverses its direction of motion
stops at 1-2s and continues further without change of direction.
Step by step video & image solution for A particle moves along a straight line and its position as a function of time is given by x = t6(3) - 3t6(2) +3t +3, then particle by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - RACEEXERCISE - RACE 196videos
RACE
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Race 215videos
RACE
- BOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
Similar Questions
Acceleration-velocity graph of a moving particle is shown in figure. The particle is
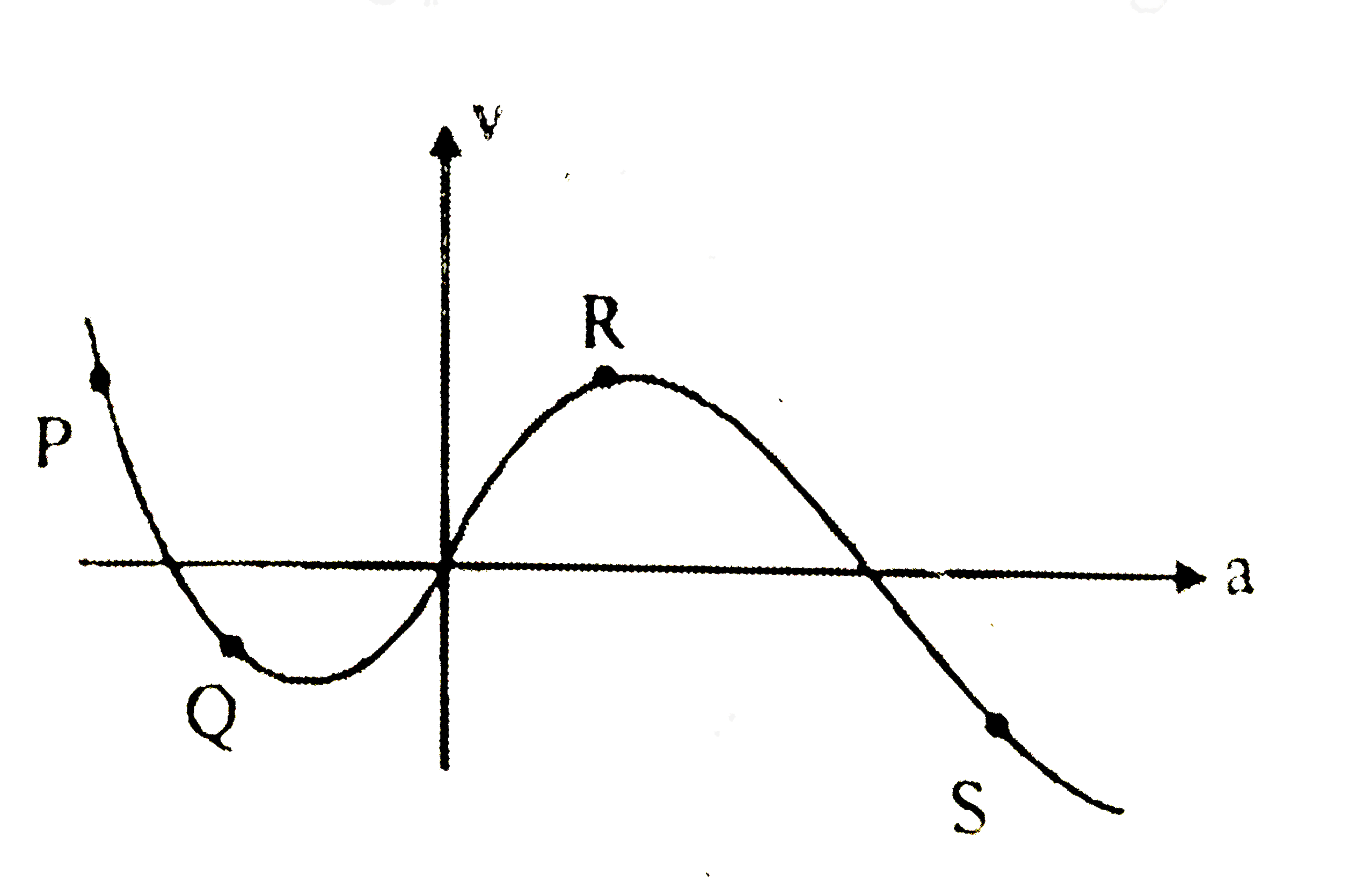 03:14View Solution
03:14View SolutionTwo projectiles are projected with velocity vA,vB at angles θA (from horizontal) and θB (from vertical) as shown in the figure below, such that vA>vB but having same horizontal component of velocity. Which of the following is correct ?
 03:00View Solution
03:00View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.01:40View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
03:32View SolutionA particle moves along a straight line. Its position at any instant is given by x = 32t-(8t^3)/3 where x is in metres and t in seconds. Find the acceleration of the particle at the instant when particle is at rest.
02:28View SolutionA particle moves along a straight line such that its displacement s at any time t is given by s=t3−6t2+3t+4m, t being is seconds. Find the velocity of the particle when the acceleration is zero.
02:39View SolutionA particle moves along a straight line such that its displacement at any time t is given by s = 3t^(3)+7t^(2)+14t + 5 . The acceleration of the particle at t = 1s is
View SolutionThe position of a particle moving in a straight line is given by x=3t^(3)-18t^(2)+36t Here, x is in m and t in second. Then
02:59View SolutionA particle moves along a straight line such that its positionx at any time t is x=3t2−t3, where x is in metre and t in second the
04:25View SolutionThe position of a particle moving along a horizontal line of any time t is given by s(t)=3t2−2t−8. The time at which the particle is at rest is
01:46View SolutionA particle moves along x-axis so that its position is given by x=2t3−3t2 at times t seconds. What is the time interval during which the particle will be on the negative half of the axis ?
01:33View SolutionA particle moves along the x-axis so that its position is given x=2t3–3t2 at a time t second. What is the time interval duringwhich particle will be on the negative half of the axis?
01:39View SolutionThe displacement of a particle moving along a straight line is given by
s=3t^(3)+2t^(2)-10t. find initial velocity and acceleration of particle.03:18View SolutionThe position of a particle moving along a horizontal line of any time t is given by s(t)=3t2−2t−8. The time at which the particle is at rest is …………….. .
03:03View SolutionThe position of a particle moving along a straight line is given by x =2 - 5t + t ^(3). Find the acceleration of the particle at t =2 s. (x is metere).
01:29View SolutionThe position of a particle moving along a. straight line is given by x=2−5t+t3 The acceleration of the particle at t = 2 sec. is ...... Here x is in meter.
02:14View Solution

