The XIth class students of ALLEN designed a rocket. The rocket was launched from cycle stand of ALLEN straight up into the air. At t=0, the rocket is at y=0 with Vy(t=0)=0. The velocity of the rocket is given by: Vy=(24t−3t2)m/s for 0≤t≤tb where tb is the time at which fuel burns out. vertically upward direction is taken as positive. (g=10m/s2)
The displacement of the rocket till the fuel burns out (t=tb) is Solution in Gujrati
128 m
486m
203m
242m
Step by step video & image solution for The XI^(th) class students of ALLEN designed a rocket. The rocket was launched from cycle stand of ALLEN straight up into the air. At t = 0, the rocket is at y = 0 with V_(y) (t = 0) = 0. The velocity of the rocket is given by: V_(y) = (24t - 3t^(2))m//s for 0 le t le t_(b) where t_(b) is the time at which fuel burns out. vertically upward direction is taken as positive. (g = 10m//s^(2)) The displacement of the rocket till the fuel burns out (t = t_(b)) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - RACE 19
6 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Race 21
5 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Acceleration-velocity graph of a moving particle is shown in figure. The particle is
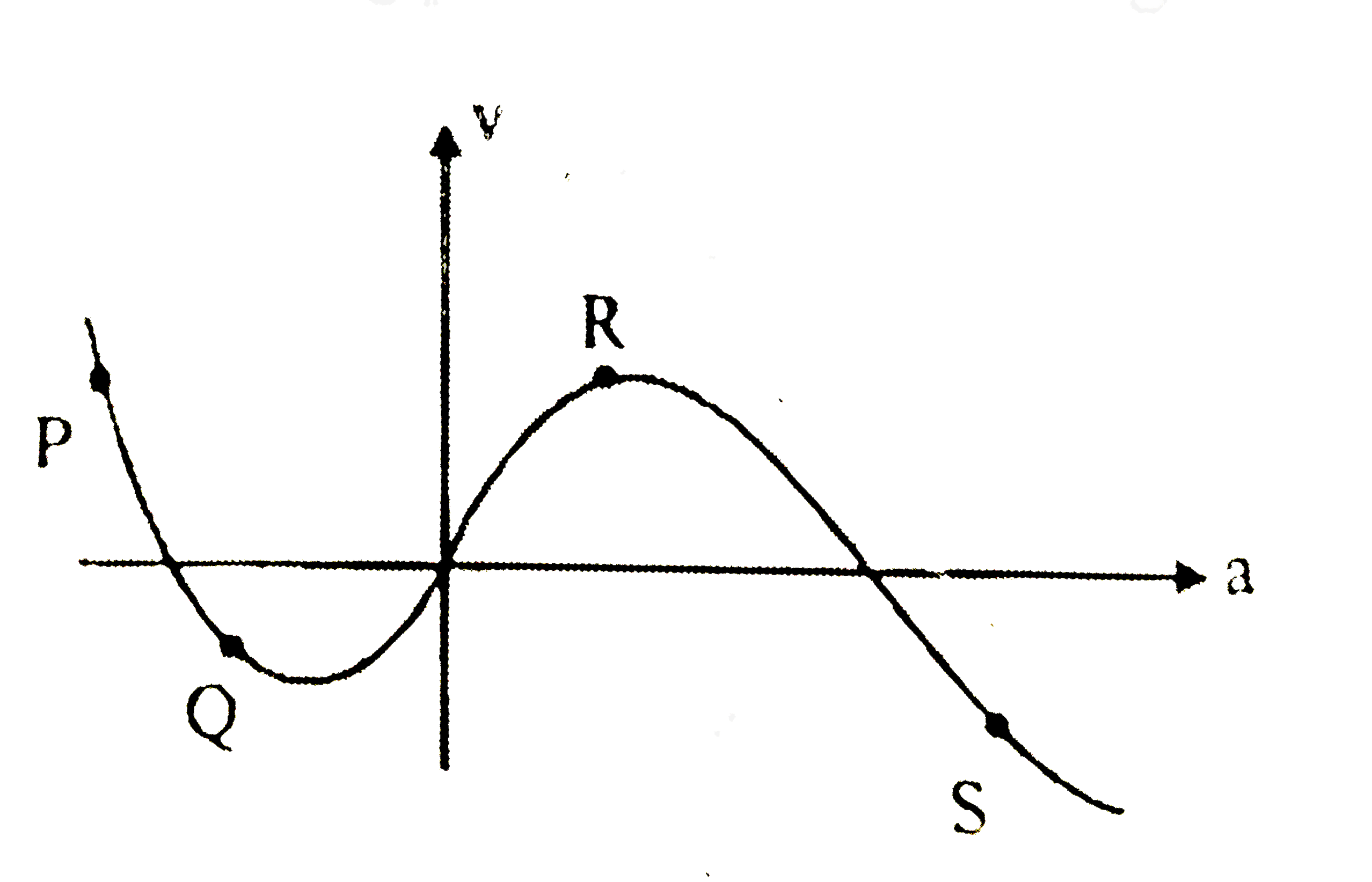
View SolutionTwo projectiles are projected with velocity vA,vB at angles θA (from horizontal) and θB (from vertical) as shown in the figure below, such that vA>vB but having same horizontal component of velocity. Which of the following is correct ?

View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View Solution(a) An unpowered rocket is in flight in air. At a moment the tracking radar gives following data regarding the rocket. r = distance of the rocket from the radar = 4000m, (dr)/(dt) = 0,(d theta)/(dt) = 1.8 "deg"//sec , where theta is the angle made by position vector of the rocket with respect to the vertical. (a) Neglect atmospheric resistance and take g = 9.8 m//s^(2) at the concerned height. Neglect height of radar. Calculate the height of the rocket above the ground. (b) Two points A and B are moving in X - Y plane with constant velocity of V_(A)= (6hati - 9 hatj ) m//s and V_(B) = (hati+hatj) m//s respectively. At time t = 0 they are 15 m apart and both of them lie on y axis with A lying away on positive Y axis with respect to B. What is the angular velocity of A with respect to B at t = 1 s ?
View SolutionA rocket prototype is fired from ground at time t=0 and it goes straight up. Take the launch point as origin and vertically upward direction as positive x direction. The acceleration of the rocket is given by
a=g2−kt2,0<t≤t0
=−g,t>t0
Where t0=√3g2k
(a) Find maximum velocity of the rocket during the up journey.
(b) Find maximum height attained by the rocket.
(c) Find total time of flight.
View SolutionThe XIth class students of ALLEN designed a rocket. The rocket was launched from cycle stand of ALLEN straight up into the air. At t=0, the rocket is at y=0 with Vy(t=0)=0. The velocity of the rocket is given by: Vy=(24t−3t2)m/s for 0≤t≤tb where tb is the time at which fuel burns out. vertically upward direction is taken as positive. (g=10m/s2)
The expression for the acceleration ay(t) valid at all times in the interval 0<t<tb is
View SolutionThe XIth class students of ALLEN designed a rocket. The rocket was launched from cycle stand of ALLEN straight up into the air. At t=0, the rocket is at y=0 with Vy(t=0)=0. The velocity of the rocket is given by: Vy=(24t−3t2)m/s for 0≤t≤tb where tb is the time at which fuel burns out. vertically upward direction is taken as positive. (g=10m/s2)
The time taken for rocket to reach its maximum height is
View SolutionA particle of mass m is moving with constant velocity v_(0) along the line y=b . At time t=0 it was at the point (0,b) . At time t=(b)/(v_(0)) , the
View SolutionThe equation of motion of rockets are x=2t,y=−4t,z=4t where the time 't' is given in second and the coordinate of a moving point in kilometres. What is the path of the rockets? At what distance will the rocket be from the starting point O(0,0,0) in 10s.
View SolutionA model rocket is launched from the ground. The height 'h' reached by the rocket after t seconds from lift off is given by h(t) = -5t2+100t,0≤t≤20. At what time the rocket is 495 feet above the ground?
View SolutionIf rocket engine ejects fuel at the rate mu kg/s with relative velocity v_(r) . At time t = 0, speed of rocket is u. Consider the value of acceleration due to gravity is constant and equal to g. Find velocity of rocket as function of time.
View SolutionIf rocket engine ejects fuel at the rate μ kg/s with relative velocity vr. At time t = 0, speed of rocket is u. Consider the value of acceleration due to gravity is constant and equal to g.
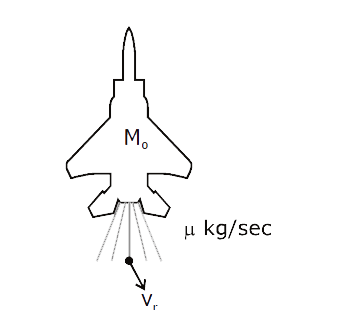
If rocket is in gravity free space then find velocity of rocket as function of time.
View SolutionThe velocity v of mass m of a rocket at time t is given by the equation :
mdvdt+Vdmdt=0,
where 'V' is the constant velocity of emission. If the rocket starts from rest when t=0 with mass m, prove that :
v=Vlog(m0m).
View Solutiont = 0 पर एक रॉकेट पृथ्वी की सतह से ऊर्ध्वाधर ऊपर की ओर 9.8 मी/से2 त्वरण से गति करना प्रारम्भ करता है। t = 0 पर ही रोकेट के सापेक्ष शून्य चाल से एक प्रेक्षेप्य को रॉकेट से छोड़ा जाता है। प्रक्षेप्य का त्वरण होगा (g = 9.8 मी/से2)
View SolutionThe equation of motion of rockets are x=2t, y=-4t, z=4t where the time 't' is given in second and the coordinate of a moving point in kilometres. What is the path of the rockets? At what distance will the rocket be from the starting point O(0, 0, 0) in 10s.
View Solution
