If r lt s lt p are in arithmetic progression, then both roots of the quadratic equation (r+2s−3p)x2+(s+2p−3r)x+(p+2r−3s)=0 are Solution in Gujrati
real
positive
negative
rational
The correct Answer is:A,B,D
Step by step video & image solution for If r lt s lt p are in arithmetic progression, then both roots of the quadratic equation (r+2s-3p)x^2+(s+2p-3r)x+(p+2r-3s)=0 are by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - MATHEMATICS34videos
TEST PAPER
- BOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS SECTION-I20videos
TEST PAPER
- BOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - Chemistry95videos
TEST PAPER
- BOOK - ALLEN CHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)10videos
SEQUENCE AND PROGRESSION
- BOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - MATHEMATICS136videos
TEST PAPERS
Similar Questions
5∑k=01sin[(K+1)θ]sin[(K+2)θ] can be equal to
02:44View SolutionGiven arrangement is in equilibrium and elongation in spring is 1cm. Tension in string AD is T1, in string BD is T2 and is string CD is T3.Choose correct values of T1,T2andT3:
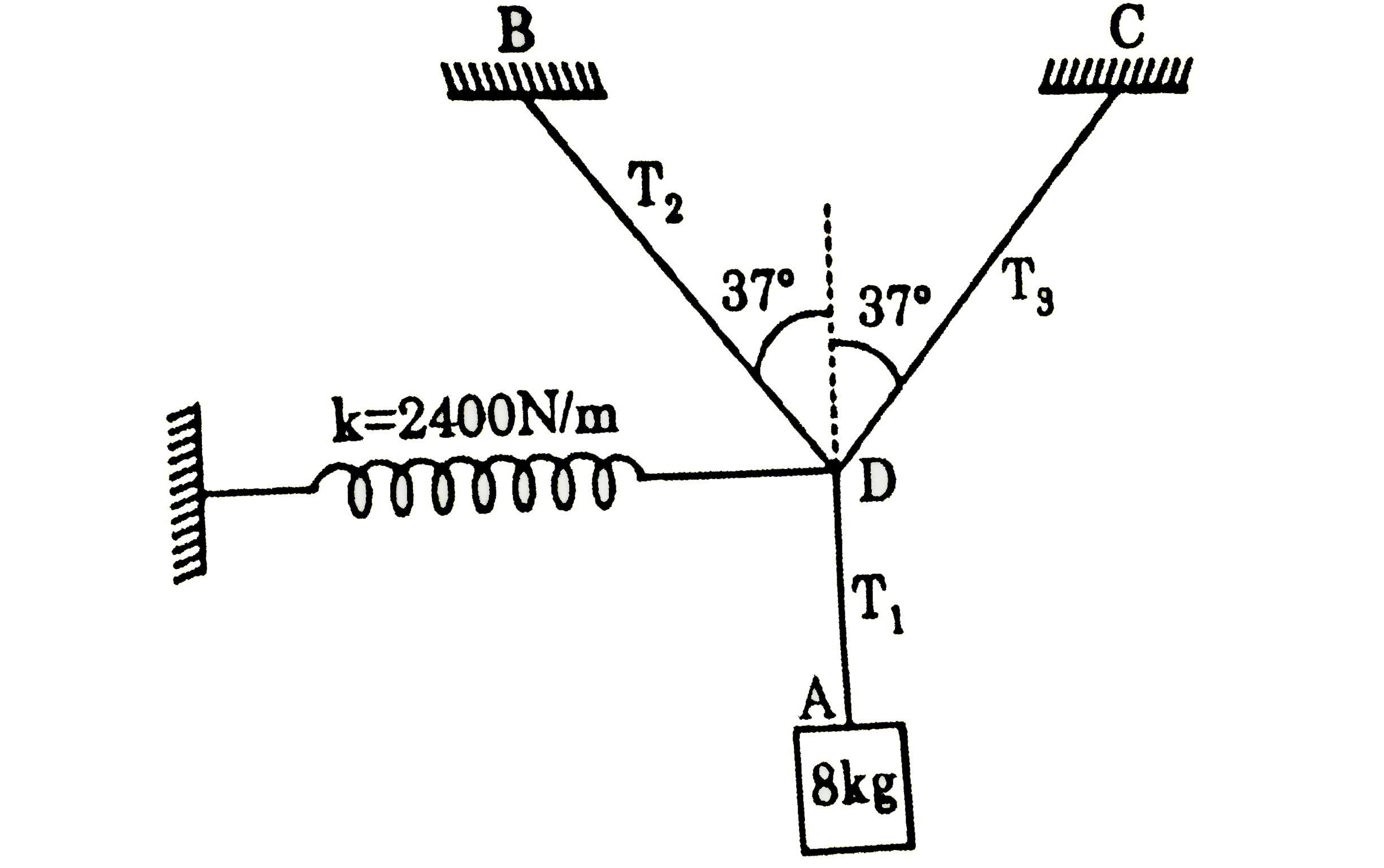 01:27View Solution
01:27View SolutionWhich of the following statement(s) is/are correct
06:00View SolutionThe minimum value of the sum of real numbers a−5,a−4,3a−3,1,a8 and a10 with a>0 is
03:11View SolutionIf a be sum of the odd numbered terms and b the sum of even numbered terms of the expansion (1+x)n,n ε N then (1−x2)n is equal to
04:26View SolutionLet pandq be the roots of the equation x2−2x+A=0 and let rands be the roots of the equation x2−18x+B=0. If p<q<r<s are in arithmetic progression, then A= and B=... (1997, 2M)
03:57View SolutionWhich of the following is(are) correct for if atom ? 1s lt 2s lt 2p lt 3s lt 3p 1s lt 2s = 2p lt 3s = 3p 1s lt 2p lt 3d lt 4s 1s lt 2s lt 4s lt 3d The correct choice is
View SolutionIf p,q,r each are positive rational number such tlaht p>q>r and the quadratic equation (p+q−2r)x2+(q+r−2p)x+(r+p−2q)=0 has a root in (−1,0) then which of the following statement hold good? (A) r+pq<2 (B) Both roots of given quadratic are rational (C) The equation px2+2qx+r=0 has real and distinct roots (D) The equation px2+2qx+r=0 has no real roots
04:53View SolutionFour elements P,Q,R & S have ground state electronic configuration as:
P→1s22s22p63s23p3Q→1s22s22p63s23p1R→1s22s22p63s23p63d104s24p3S→1s22s22p63s23p63d104s24p1
Comment which of the following option represent the correct order of true (T) & false (F) statement I size of P< size of Q II size of R< size of S
III size of P< size of R (appreciable difference) IV size of Q< size of S (appreciable difference)02:19View SolutionFour elements P,Q,R & S have ground state electronic configuration as: {:(P rarr 1s^(2) 2s^(2) 2p^(6) 3s^(2) 3p^(3),Q rarr 1s^(2) 2s^(2)2p^(6)3s^(2)3p^(1)),(R rarr 1s^(2) 2s^(2)2p^(6)3s^(2)3p^(6)3d^(10)4s^(2)4p^(3),S rarr 1s^(2)2s^(2)2p^(6)3s^(2)3p^(6)3d^(10)4s^(2)4p^(1)):} Order of IE_(1) values among the following is
04:40View SolutionIf r lt s lt p are in arithmetic progression, then both roots of the quadratic equation (r+2s−3p)x2+(s+2p−3r)x+(p+2r−3s)=0 are
View SolutionIf p,q are roots of the quadratic equation x2−10rx−11s=0andr,s are roots of x2−10px−11q=0 then find the value of p+q +r+s.
01:51View SolutionLet p and q be the roots of x2−2x+A=0 and let r and s be the roots of x2−18+B=0. If p<q<r<s are in ordered pair (A , B) =
03:54View SolutionIf p,q,r,s are rational numbers and the roots of f(x)=0 are eccentricities of a parabola and a rectangular hyperbola, where f(x)=px3+qx2+rx+s ,then p+q+r+s= a. p b. −p c. 2p d. 0
05:50View Solutionमाना 'p' एवं 'q' समीकरण x2−2x+A=0 के मूल है तथा 'r' एवं 's' समीकरण x2−18x+B=0 के मूल है। यदि p<q<r<s समान्तर श्रेणी में है, तो (A+ B) का मान ज्ञात कीजिये।
04:41View SolutionLet p and q be the roots of the equation x2−2x+A=0 and let r and s be the roots of the equation x2−18x+B=0.ifpltqltrlts are in arithmetic progression, then A,B respectively equal to
02:28View Solution

