If s=ut+12at2, where u and a are constants. Obtain the value of dsdt. Solution in Gujrati
The correct Answer is:3000 volt
VA=KQ2−KQ3VB=KQ3−KQ2VA−VB=2(KQ2−KQ3)
=9×109×10−6(1−23)=3000 volt
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - PHY
68 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - EXERCISE-2
80 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Comprehension 9
2 Videos
- AIIMS 2019BOOK - ALLEN CHAPTER - AIIMS 2019EXERCISE - PHYSICS
39 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
A circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
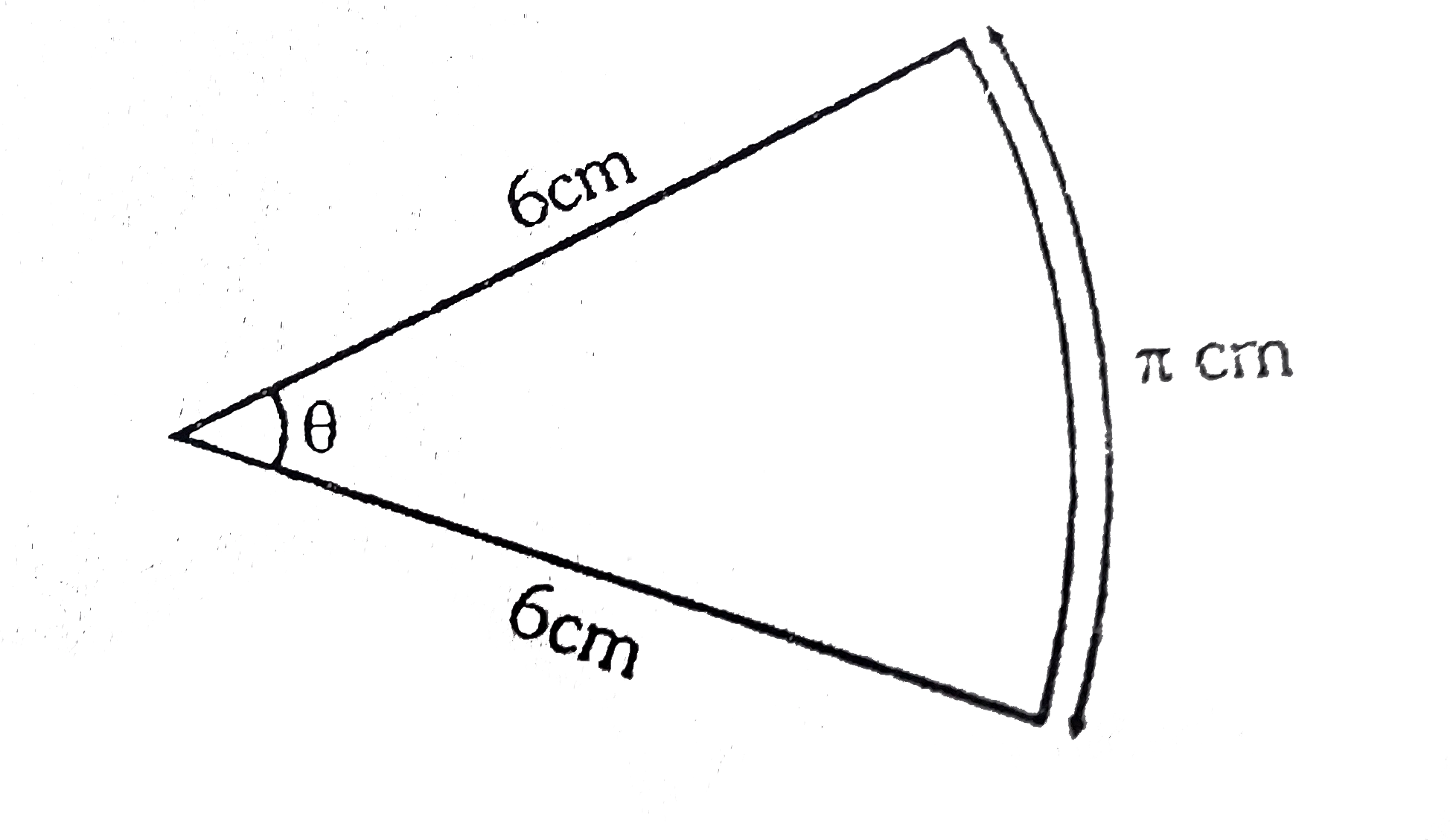
View SolutionThe equation of a curve is given as y=x2+2−3x.
The curve intersects the x-axis at
View SolutionA physical quantity is given by X=[MaLbTc]. The percentage error in measurement of M,L and T are α,β,γ respectively. Then the maximum % error in the quantity X is
View SolutionA simple pendulum executing SHM in a straight line has zero velocity at 'A' and 'B' whose distances form 'O' in the same line OAB are 'a' and 'b'. If the velocity half wat between them is 'v' then its time period is
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (radian/s) is -
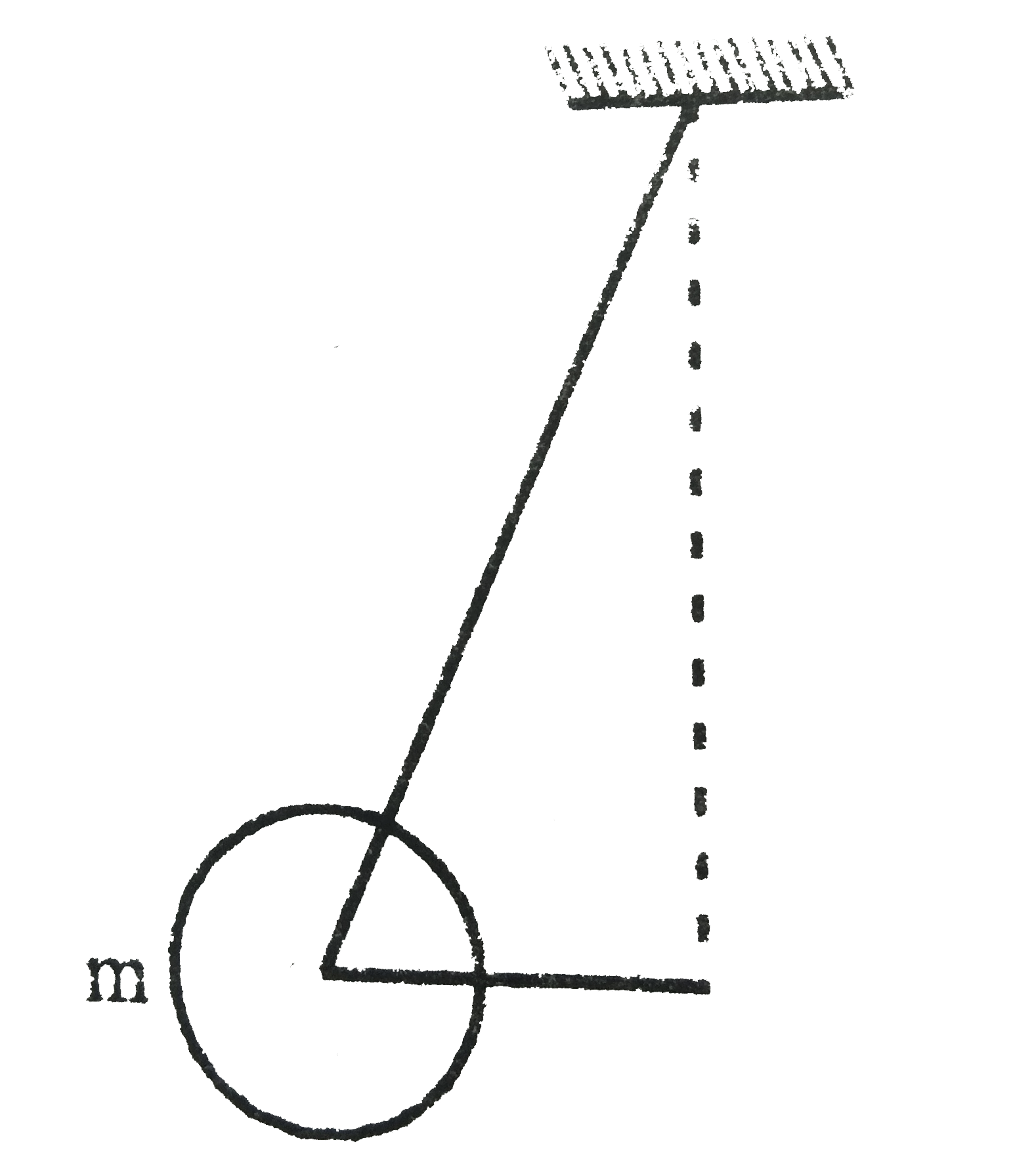 .
.
View SolutionIn s=ut+12at2, if s=16m,t=2 seconds and a=5m/s2, then find the value of u by making u as the subject.
View SolutionFind the degree of the following :
(1+dsdt)32=5d2sdt2
View Solutionग्राफ़िय विधि से साबित करे कि s=ut+12at2, जहाँ s , u, a और t अपना सामान्य अर्थ रखते है ।
View Solutionसमीकरणों की कोटि तथा घात लिखिये s2d2tds2+stdtds=s
View SolutionIf s=at2+bt+c find the value of [dsdt]t=1 .
View SolutionS=12log(1+t1−t) হলে প্রমাণ করো যে,
(dsdt).(dtds)=1
View Solutions=12log(1+t1−t) হলে প্রমাণ করো যে,
d2sdt2=(dsdt)3.d2tds2
View SolutionS=12log(1+t1−t) হলে প্রমাণ করো যে,
(dsdt).(dtds)=1
View SolutionS=12log(1+t1−t) হলে প্রমাণ করো যে,
d2sdt2=−(dsdt)3.(d2tds2)
View SolutionFind the order and degree of the differential equation t2d2sdt2−stdsdt=s
View Solution(dsdt)4+3sd2sdt2=0
View Solution
