A particle is projected with a velocity 10ms at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.Solution in Gujrati
The correct Answer is:1.6 m, 8 m.
y=xtanθ−gx22u2cos2θ
for y=1,θ=37∘,u=10m/s
1=34x−10x22×100×(1625)
1=34x−564x2
5x2−48x+64=0
5x2−40x−8x+64=0
x=8m,1.6m
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
The vertical height y and horizontal distance x of a projectile on a certain planet are given by x=(3t)m,y=(4t−6t2) m where t is in seconds, Find the speed of projection (in m/s).
View SolutionA particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA particle is thrown with a velocity 10m/s and its horizontal range is 5m. Find angle/angles of the projection.
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.

View SolutionA particle is projected with a speed of 10m/s at an angle 37∘ from horizontal, anglular speed to particle with respect to point of projection at t=0.5sec. Is (16X61) rad/sec then calculate X :
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA particle is projected from the ground with some initial velocity making an angle of 45∘ with the horizontal. It reaches a height of 7.5 m above the ground while it travels a horzontal distance of 10 m from the point of projection . Find the initial speed of projection ( g = 10 m/s2) .
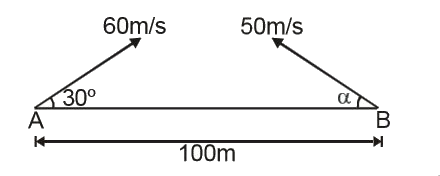
View SolutionA particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
View SolutionHorizontally 30^@ A particle of mass m is projected from the velocity v at an angle. When the particle is at its maximum height h, the magnitude of the particle's angular momentum relative to the point of projection is
View SolutionA particle is projected from the ground with an initial speed of 5ms−1 at an angle of projection 60° with horizontal. The average velocity of the particle between its time of projection and the time it reaches highest point of trajectory
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with a velocity v at an angle 60^@ with horizontal . When the particle is at maximum height the magnitude of it's angular momentum about the point of projection is
View SolutionA particle from the horizontal 30^@ Is projected at a velocity of 20 m / s at an angle of: (g = 10 m//s^2) Find the position vector after 1 second of the particle. (Consider projectile as root point)
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution
