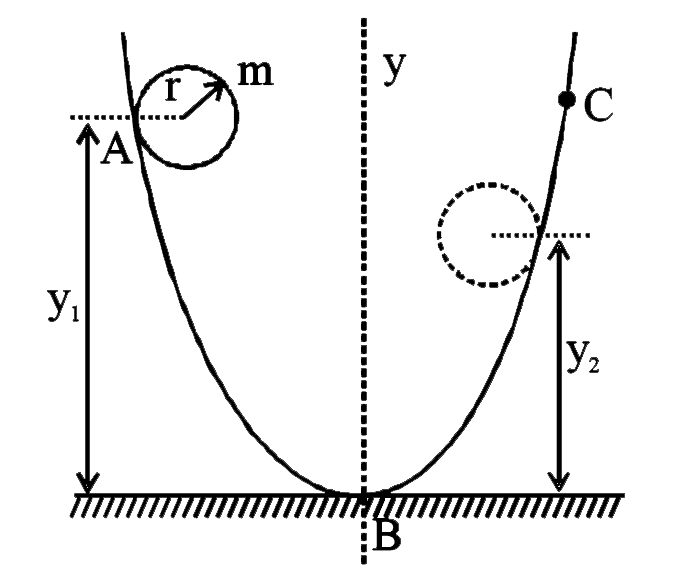
A uniform disck rolls from rest from height $y_{1}$ down the side of a fixed trough whose vertical dimension $y$ is given by the equation $y = k x^{2}$ . The disc does not slip from A to B, but the surface of the trough is frictionless from B C (see figure). The disc reaches height $y_{2}$ . $\frac{3 y_{2}}{y_{1}}$ is (Assume radius of disc to be very small compared to $y_{1}$ & $y_{2}$ )
Solution in Gujrati

In rock salt structure $a = 2 (r_{cation} + r_{anion})$ . Where $a =$ edge length of cube

In $C s C l$ structure $a = \frac{2}{\sqrt{3}} (r_{cation} + r_{anion})$ . Where $a =$ edge length of cube

In antifluorite structure $a = \frac{4}{\sqrt{3}} (r_{cation} + r_{anion})$ . Where $a =$ edge length of cube

In $N a C l$ structure $a = \frac{2}{\sqrt{3}} (r_{cation} + r_{anion})$ . When $a =$ edge length of cube

Video Solution

Answer

Step by step video & image solution for A uniform disck rolls from rest from height y_(1) down the side of a fixed trough whose vertical dimension y is given by the equation y=kx^(2). The disc does not slip from A to B, but the surface of the trough is frictionless from B C (see figure). The disc reaches height y_(2). (3y_(2))/(y_(1)) is (Assume radius of disc to be very small compared to y_(1) & y_(2)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

ALLEN -TEST PAPERS-CHEMISTRY