A function has the form f(x)=ax+b, where a and b are constants. If f(2)=1 and f(−3)=11, the function is defined by Solution in Gujrati
f(x)=2x+5
f(x)=2x−5
f(x)=−2x+5
f(x)=−2x+5
The correct Answer is:C
Step by step video & image solution for A function has the form f(x)=ax+b, where a and b are constants. If f(2)=1" and "f(-3)=11, the function is defined by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (VECTORS)
62 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
37 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Graphs))
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
State whether the following relations are true or false
(1)−−→AB=−−→BA
(2)−−→AB=−−−→BA
(3)∣∣∣−−→AB∣∣∣=∣∣∣−−→BA∣∣∣
(4)∣∣∣−−→AB∣∣∣=∣∣∣−−−→AB∣∣∣
(5)ˆj=ˆk
(6)∣∣ˆj∣∣=∣∣ˆk∣∣
View SolutionWhich one of the following is not a fundamental quantity ?
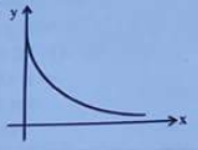
View SolutionWhich of the following equation is best representation of following graph's?
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionFind the values of a and b such that the function defined by f(x)=⎧⎪⎨⎪⎩5ifx≤2ax+bif2<x<1021ifx≥10 is a continuous function.
View SolutionLet f:A→B be a function defined as f(x)=2x+3x−3, where A=R-{3} and B=R-{2}. Is the function f one-one and onto ? Is f invertible ? If yes, then find its inverse.
View SolutionLet f(x)=ax2−b|x| , where a and b are constant . Then at x=0 , f(x) has
View Solutionमान लीजिए कि f={(1,1),(2,3),(0,−1),(−1,−3)} Z से Z में, f(x)=ax+b द्वारा परिभाषित एक फलन है, जहाँ a, b कोई पूर्णाक है। a, b को निर्धारित कीजिए।
View Solutionसिद्ध कीजिये कि फलन f(x)=ax+b , जहाँ a व b एक अचर है तथा a>0,R पर एक वर्धमान फलन है
View SolutionIf f={(0,−1),(−1,−3),(2,3),(3,5)} is a function from z to z defined by f(x)=ax+b. Then,
View SolutionIf the function f:{−1,1}→{0,2}, defined by f(x)=ax+b is a surjection, then find a & b.
View SolutionA function is defined as f(x)=ax2–b|x| where a and b are constants then at x = 0 we will have a maxima of f(x) if
View SolutionDetermine a quadratic function (f) is defined by f(x)=ax2+bx+c. If f(0)=6,f(2)=11,f(-3)=6
View SolutionThe function f:C→C defined by f(x)=ax+bcx+d for x∈C, where bd≠0 reduces to a constant function, if
View Solutionਮੰਨ ਲਉ ਕਿ [a,b] ਤੇ ਪਰਿਭਾਸ਼ਿਤ ਇੱਕ ਫਲਨ f ਇਸ ਤਰ੍ਹਾਂ x∈(a,b) ਦੇ ਲਈ f'(x)>0 ਹੈ ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ (a,b) ਤੇ f ਵਧਦਾ ਫਲਨ ਹੈ।
View Solution