A particle is moving along a straight line parallel to x-axis with constant velocity and position vector is vtˆi+bˆj. Find angular momentum about the origin in vector form : Solution in Gujrati
+mv2bˆk
−mvbˆk
−2mvbˆk
+mvbˆj
The correct Answer is:B
Step by step video & image solution for A particle is moving along a straight line parallel to x-axis with constant velocity and position vector is vthati+bhatj. Find angular momentum about the origin in vector form : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)
25 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
20 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )
12 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two paricles of equal mass m go round a circle of radius R under the action of their mutual gravitional attraction. The speed of each particle is
View SolutionA cable that can support a load W is cut into two equal parts .T he maximum load that can be supported by either part is
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionA mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

View SolutionA particle is moving in the xy-plane with a constant velocity along a line parallel to the X-axis away from the origin. The magnitude of its angular momentum about the origin.
View SolutionA particle is moving with a contant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect of the origin is
View SolutionA body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
View SolutionA body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Calculate its angular momentum with respect to the origin?
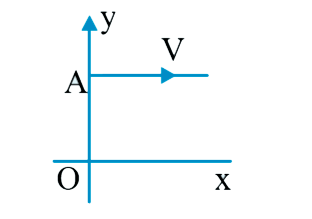
View SolutionA particle is moving with a contant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect of the origin is
View SolutionA particle is moving with a contant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect of the origin is
View SolutionA particle moves parallel to X-axis as shown in the figure such that at all instant the y axis component of its position vector is constant and is equal to 'b'. The angular velocity of the particle about the origin is
View SolutionA particle of mass m is moving with a uniform velocity along a straight path parallel to the x -axis. Angular momentum of the particle with respect to the origin will be
View SolutionA particle of mass m is moving on the XY-plane along a straight line y = d, with constant velocity v. Its angular momentum about the origin
View Solution
