If a unit positive charge is taken from one point to another over an equipotential surface ,then
work is done one the charge
work is doen by the charge
work done is constant
no work is done
The correct Answer is:D
To solve the question, we need to understand the concept of equipotential surfaces and the work done when moving a charge across these surfaces.
1. Understanding Equipotential Surfaces:
- An equipotential surface is a surface where the electric potential is the same at every point. This means that if a charge moves along this surface, there is no change in electric potential energy.
2. Identifying the Charge and Movement:
- We are given a unit positive charge (let's denote it as Q=+1C) that is being moved from one point (Point 1) to another point (Point 2) along an equipotential surface.
3. Change in Electric Potential (ΔV):
- Since the charge is moving along an equipotential surface, the electric potential at Point 1 and Point 2 is the same. Therefore, the change in electric potential is:
ΔV=V2−V1=0
4. Calculating Work Done:
- The work done W in moving a charge Q through a potential difference ΔV is given by the formula:
W=Q⋅ΔV
- Substituting the values we have:
W=1C⋅0=0J
5. Conclusion:
- The work done in moving a unit positive charge from one point to another over an equipotential surface is zero. Thus, the answer to the question is:
Work Done=0J
Final Answer:
The work done is 0 Joules.
---
- An equipotential surface is a surface where the electric potential is the same at every point. This means that if a charge moves along this surface, there is no change in electric potential energy.
- We are given a unit positive charge (let's denote it as Q=+1C) that is being moved from one point (Point 1) to another point (Point 2) along an equipotential surface.
- Since the charge is moving along an equipotential surface, the electric potential at Point 1 and Point 2 is the same. Therefore, the change in electric potential is:
ΔV=V2−V1=0
- The work done W in moving a charge Q through a potential difference ΔV is given by the formula:
W=Q⋅ΔV
- Substituting the values we have:
W=1C⋅0=0J
- The work done in moving a unit positive charge from one point to another over an equipotential surface is zero. Thus, the answer to the question is:
Work Done=0J
The work done is 0 Joules.
Similar Questions
Knowledge Check
When a positive q charge is taken from lower potential to a higher potential point, then its potential energy will
Aremin the sameBincreaseCdecreaseDbecome zeroThe ability to move from one point to another in the shortest period of time:
APowerBAgilityCSpeedDBalanceThe work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
AWQxBWCWxDWQ
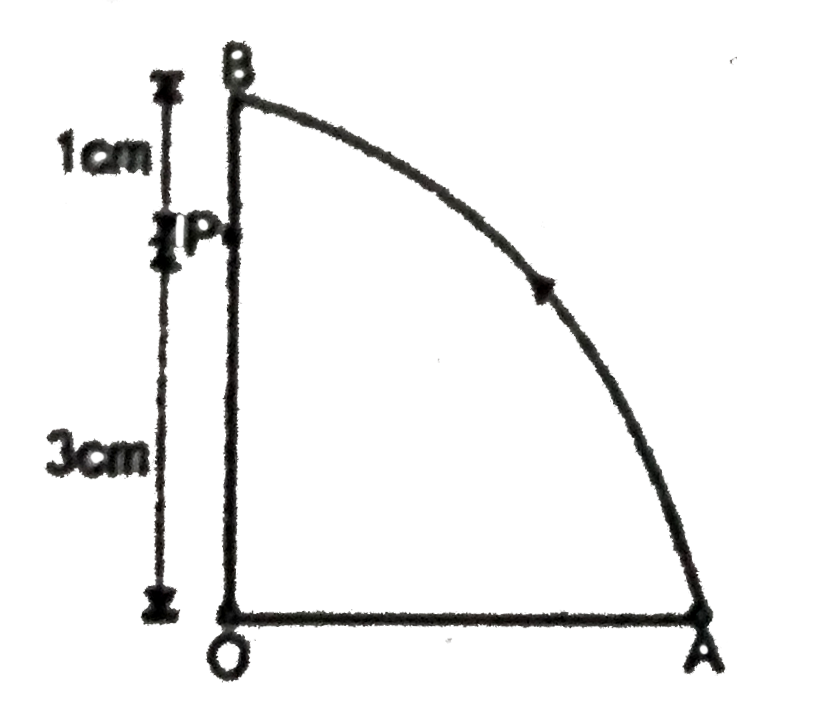
A point charge of 5C is placed at point P (as shown in figure). A unit positive charge is taken from A to B along the circular path shown, then the net work done by electrostatic force is : [O is the centre of the circular path] [Where k=9×109Nm2/C2]
View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB. The initial temperature at A is T0. Calculate the heat abosrbed by the gas in the process A→C→B.

View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB. The initial temperature at A is T0. Calculate the heat abosrbed by the gas in the process A→C→B.

View SolutionNature of equipotential surface for a point charge is
View SolutionWork done by an electrostatic field in moving a given charge from one point to another …… upon the chosen closed path.
View Solution
