We wish to see inside an atom. Assuming the atom to have a diameter of 100 pm, this means that one must be able to resolve a width of say 10 pm. If an electron microscope is used, the minimum electron energy required is about
1.5 keV
15 KeV
150 keV
1.5 MeV.
The correct Answer is:B
To solve the problem of determining the minimum electron energy required to resolve a width of 10 pm using an electron microscope, we can follow these steps:
Step 1: Understand the relationship between wavelength and resolution
The resolving power of an electron microscope is related to the wavelength of the electrons used. To resolve a feature of size d, the wavelength λ must be comparable to or smaller than d. In this case, we want to resolve a width of 10 pm (picometers).
Step 2: Convert units
Convert the width from picometers to meters for calculation:
10 pm=10×10−12 m=10−11 m
Step 3: Use the de Broglie wavelength formula
The de Broglie wavelength λ of an electron is given by:
λ=h√2meE
where:
- h is Planck's constant (6.63×10−34Js),
- me is the mass of the electron (9.11×10−31kg),
- E is the energy of the electron.
Step 4: Rearrange the formula to find energy
Rearranging the formula to solve for energy E:
E=h22meλ2
Step 5: Substitute values into the equation
Substituting the known values into the equation:
E=(6.63×10−34)22×(9.11×10−31)×(10−11)2
Step 6: Calculate the energy
Calculating the numerator:
(6.63×10−34)2=4.39×10−67 J2
Calculating the denominator:
2×(9.11×10−31)×(10−11)2=2×9.11×10−31×10−22=1.82×10−52 J
Now substituting these values back into the energy equation:
E=4.39×10−671.82×10−52≈2.41×10−15 J
Step 7: Convert energy to electron volts
To convert joules to electron volts, use the conversion factor 1 eV=1.6×10−19 J:
E≈2.41×10−151.6×10−19≈15.06 keV
Conclusion
The minimum electron energy required to resolve a width of 10 pm is approximately 15 keV.
---
The resolving power of an electron microscope is related to the wavelength of the electrons used. To resolve a feature of size d, the wavelength λ must be comparable to or smaller than d. In this case, we want to resolve a width of 10 pm (picometers).
Convert the width from picometers to meters for calculation:
10 pm=10×10−12 m=10−11 m
The de Broglie wavelength λ of an electron is given by:
λ=h√2meE
where:
- h is Planck's constant (6.63×10−34Js),
- me is the mass of the electron (9.11×10−31kg),
- E is the energy of the electron.
Rearranging the formula to solve for energy E:
E=h22meλ2
Substituting the known values into the equation:
E=(6.63×10−34)22×(9.11×10−31)×(10−11)2
Calculating the numerator:
(6.63×10−34)2=4.39×10−67 J2
Calculating the denominator:
2×(9.11×10−31)×(10−11)2=2×9.11×10−31×10−22=1.82×10−52 J
Now substituting these values back into the energy equation:
E=4.39×10−671.82×10−52≈2.41×10−15 J
To convert joules to electron volts, use the conversion factor 1 eV=1.6×10−19 J:
E≈2.41×10−151.6×10−19≈15.06 keV
The minimum electron energy required to resolve a width of 10 pm is approximately 15 keV.
Similar Questions
In an electron microscope, the resolution that can be achieved is of the order of the wavelength of electrons used. To resolve a width of 7.5×10−12 m, the minimum electron energy required is close to :
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
A formula analogous to Balmer's formula applies to the series of spectral lines which arise from transition from higher energy levels to the lowest energy level of hydrogen atom. Write this formula and use it to determine the ground state energy of a hydrogen atom in eV.
A 'muonic hydrogen atom' is like a hydrogen atom in which the electron is replaced by a heavier particle, the muon. The mass of a muon is about 207 times the mass of an electron, while its charge is the same as that of an electron. A muon has a very short lifetime, but we ignore its ubstable nature here.View SolutionThe heat of neutralization for a strong acid by a strong base is a constant
View SolutionA: If a beam of photons of energy 10.0 eV each is incident on a sample of hydrogen gas containing all atoms in the ground state, then the beam of the photons is completely transmitted through the gas without absorption.
R: The minimum energy required by an electron to make a transition to an excited state is 10.2eV.View Solutionde Broglie proposed dual nature for electron by putting his famous equation λ=hmv. Later on, Heisenberg proposed uncertainty principle as δpΔx≥h4π. On the contrary,
Particle nature of electron was established on the basis of photoelectric effect. When a photon strikes the metal surface it gives up its energy to the electron. Part of this energy (say W) is used by the electrons to escape from the metal and the remaining energy imparts kinetic energy (1/2mv2) to the ejected photoelectron. The potential applied on the surface to reduce the velocity of photoelectron to zero is known as stopping potential .
When a beam of photons of a particular energy was incident on a surface of a particular pure metal having work function =(40 eV), some emitted photoelectrons had stopping potential equal to 22 V. some had 12V and rest had lower values. Calculate the wavelength of incident photons assuming that at least one photoelectron is ejected with maximum possible kinetic energy :View SolutionIn a hydrogen-like atom , an electron is orbating in an orbit having quantum number n. Its frequency of revolution is found to be 13.2×1015 Hz. Energy required to move this electron from the atom to the above orbit is 54.4eV. In a time of ? nano second the electron jumps back to orbit having quantum numbern/2.If τ be the average torque acted on the electron during the above process, then find τ×1027 in Nm. (given: h/λ=2.1×10−34J−s, friquency of revolution of electron in the ground state of H atom v0=6.6×1015 and ionization energy of H atom (E0=13.6eV)
View SolutionIn a hydrogen-like atom , an electron is orbating in an orbit having quantum number n. Its frequency of revolution is found to be 13.2×1015 Hz. Energy required to move this electron from the atom to the above orbit is 54.4eV. In a time of 7 nano second the electron jumps back to orbit having quantum numbern/2.If τ be the average torque acted on the electron during the above process, then find τ×1027 in Nm. (given: h/λ=2.1×10−34J−s, friquency of revolution of electron in the ground state of H atom v0=6.6×1015 and ionization energy of H atom (E0=13.6eV)
View SolutionA point source of monochromatic light of 1.0mW is placed at a distance of 5.0m from a metal surface. Light falls perpendicularly on the surface. Assume wave theory of light to hold and also that all the light falling on the circular area with radius =1.0×10−9m(which is few times the diameter of an atom) is absorbed by a single electron on the surface. Calculate the time required by the electron to receive sufficient energy to come out of the metal if the work function of the metal is 2.0eV.
View SolutionA parallel plate capacitor is to be designed with a voltage rating 1 KV using a material of dielectric constant 3 and dielectric strength about 107Vm−1. [Dielectric strength is the maximum electric field a material can tolerate without break down, i.e, without starting to conduct electrically through partial ionization. For safety, we should like the field never to exceed say 10% of the dielectric strength]. What minimum area of the plates is required to have a capacitance of 50 pF ?
View SolutionThe ciliary muscles of eye control the curvature of the lens in the eye and hence can alter the effective focal length of the system. When the muscles are fully relaxed, the focal length is maximum. When the muscles are strained, the curvature of lens increases. That means radius of curvature decreases and focal length decreases. For a clear vision, the image must be on the retina. The image distance is therefore fixed for clear vision and it equals the distance of retina from eye lens. It is about 2.5cm for a grown up person.
A perosn can theoretically have clear vision of an object situated at any large distance from the eye. The smallest distance at which a person can clearly see is related to minimum possible focal length. The ciliary muscles are most strained in this position. For an average grown up person, minimum distance of the object should be around 25cm.
A person suffering from eye defects uses spectacles (eye glass). The function of lens of spectacles is to form the image of the objects within the range in which the person can see clearly. The image o the spectacle lens becomes object for the eye lens and whose image is formed on the retina.
The number of spectacle lens used for th eremedy of eye defect is decided by the power fo the lens required and the number of spectacle lens is equal to the numerical value of the power of lens with sign. For example, if power of the lens required is +3D (converging lens of focal length 100/3cm ), then number of lens will be +3.
For all the calculations required, you can use the lens formula and lensmaker's formula. Assume that the eye lens is equiconvex lens. Neglect the distance between the eye lens and the spectacle lens.
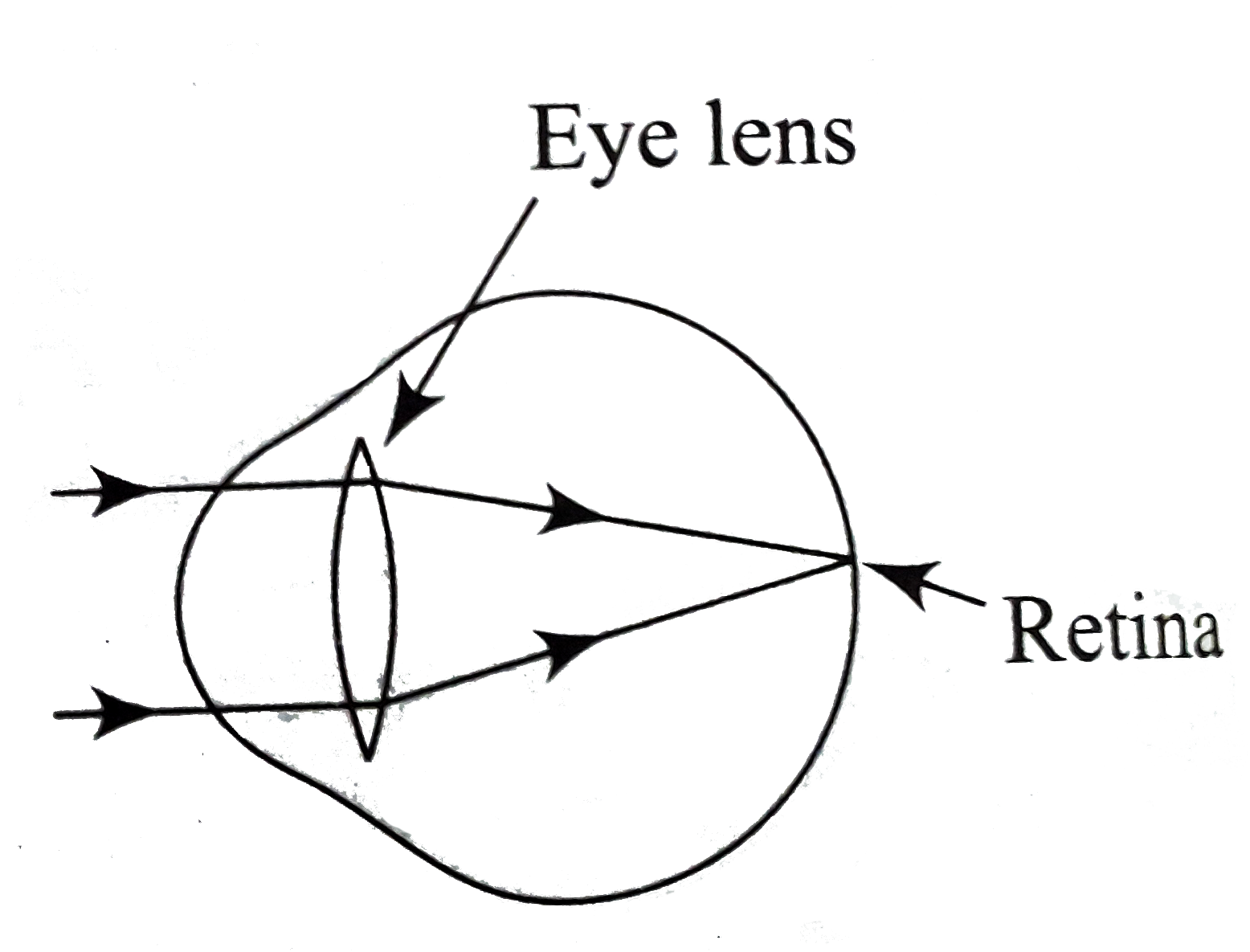
Q. A person can see objects clearly from distance 10cm to ∞. Then, we can say that the person isView Solution

