Which of the following functionss represents a simple harmonic oscillation ?
sinωt−cosωt
sin2ωt
sinωt+sin2ωt
sinωt−sin2ωt
The correct Answer is:A
To determine which of the given functions represents simple harmonic motion (SHM), we need to analyze the conditions for SHM. The key condition is that the acceleration of the oscillating particle must be directly proportional to the negative of its displacement from the equilibrium position.
1. Understand the Condition for SHM:
- For a function to represent SHM, the acceleration a must satisfy the condition:
a=−k⋅y
where k is a positive constant and y is the displacement.
2. Analyze the Given Function:
- Let's consider the function given in the question:
y=sin(ωt)−cos(ωt)
3. Calculate the Velocity:
- The velocity v is the first derivative of displacement y with respect to time t:
v=dydt=ddt(sin(ωt)−cos(ωt))
- Using the chain rule:
v=ωcos(ωt)+ωsin(ωt)
4. Calculate the Acceleration:
- The acceleration a is the derivative of velocity v:
a=dvdt=ddt(ωcos(ωt)+ωsin(ωt))
- Again, applying the chain rule:
a=−ω2sin(ωt)+ω2cos(ωt)
- This can be rewritten as:
a=ω2(−sin(ωt)+cos(ωt))
5. Check the Proportionality:
- We can factor out −ω2:
a=−ω2(sin(ωt)−cos(ωt))
- Notice that y=sin(ωt)−cos(ωt), which means:
a=−ω2y
- This satisfies the condition for SHM since a is proportional to −y.
6. Conclusion:
- Since the derived acceleration is proportional to the negative of the displacement, the function y=sin(ωt)−cos(ωt) represents simple harmonic motion.
Final Answer:
The function that represents simple harmonic oscillation is:
y=sin(ωt)−cos(ωt)
- For a function to represent SHM, the acceleration a must satisfy the condition:
a=−k⋅y
where k is a positive constant and y is the displacement.
- Let's consider the function given in the question:
y=sin(ωt)−cos(ωt)
- The velocity v is the first derivative of displacement y with respect to time t:
v=dydt=ddt(sin(ωt)−cos(ωt))
- Using the chain rule:
v=ωcos(ωt)+ωsin(ωt)
- The acceleration a is the derivative of velocity v:
a=dvdt=ddt(ωcos(ωt)+ωsin(ωt))
- Again, applying the chain rule:
a=−ω2sin(ωt)+ω2cos(ωt)
- This can be rewritten as:
a=ω2(−sin(ωt)+cos(ωt))
- We can factor out −ω2:
a=−ω2(sin(ωt)−cos(ωt))
- Notice that y=sin(ωt)−cos(ωt), which means:
a=−ω2y
- This satisfies the condition for SHM since a is proportional to −y.
- Since the derived acceleration is proportional to the negative of the displacement, the function y=sin(ωt)−cos(ωt) represents simple harmonic motion.
The function that represents simple harmonic oscillation is:
y=sin(ωt)−cos(ωt)
Similar Questions
Which of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)sinωt−cosωt (ii) sin2ωt (iii) cosωt+2sin2ωt
View SolutionAs the expression in ivolving sine function , which of the following equations does not represent a simple harmonic motion ?
View Solution
Knowledge Check
Which of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)sinωt−cosωt (ii) sin2ωt (iii) cosωt+2sin2ωtAa simple harmonic motion with a period πω.Ba simple harmonic motion with a period 2πωCa periodic, but not simple harmonic motionn with a period πωDa periodic, but not simple harmonic motion with a period 2πωWhich of the following expression does not represent simple harmonic motion?
Ax=Acosω+BsinωBx=Acos(ωt+α)Cx=Bsin(ωt+B)Dx=Asinωtcos2ωtWhich of the following energy-time graphs represents dajmped harmonic oscillator?
A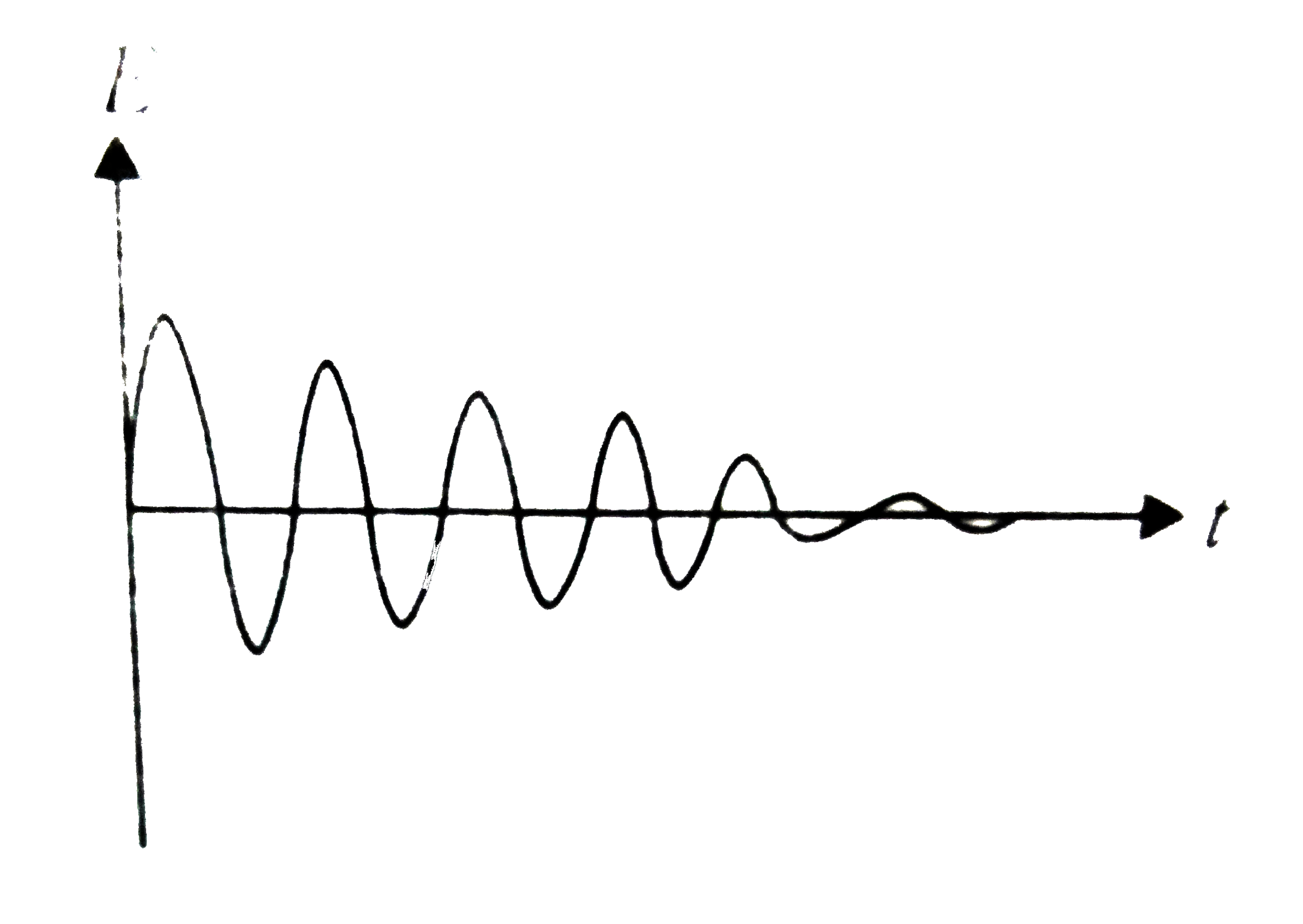 B
B C
C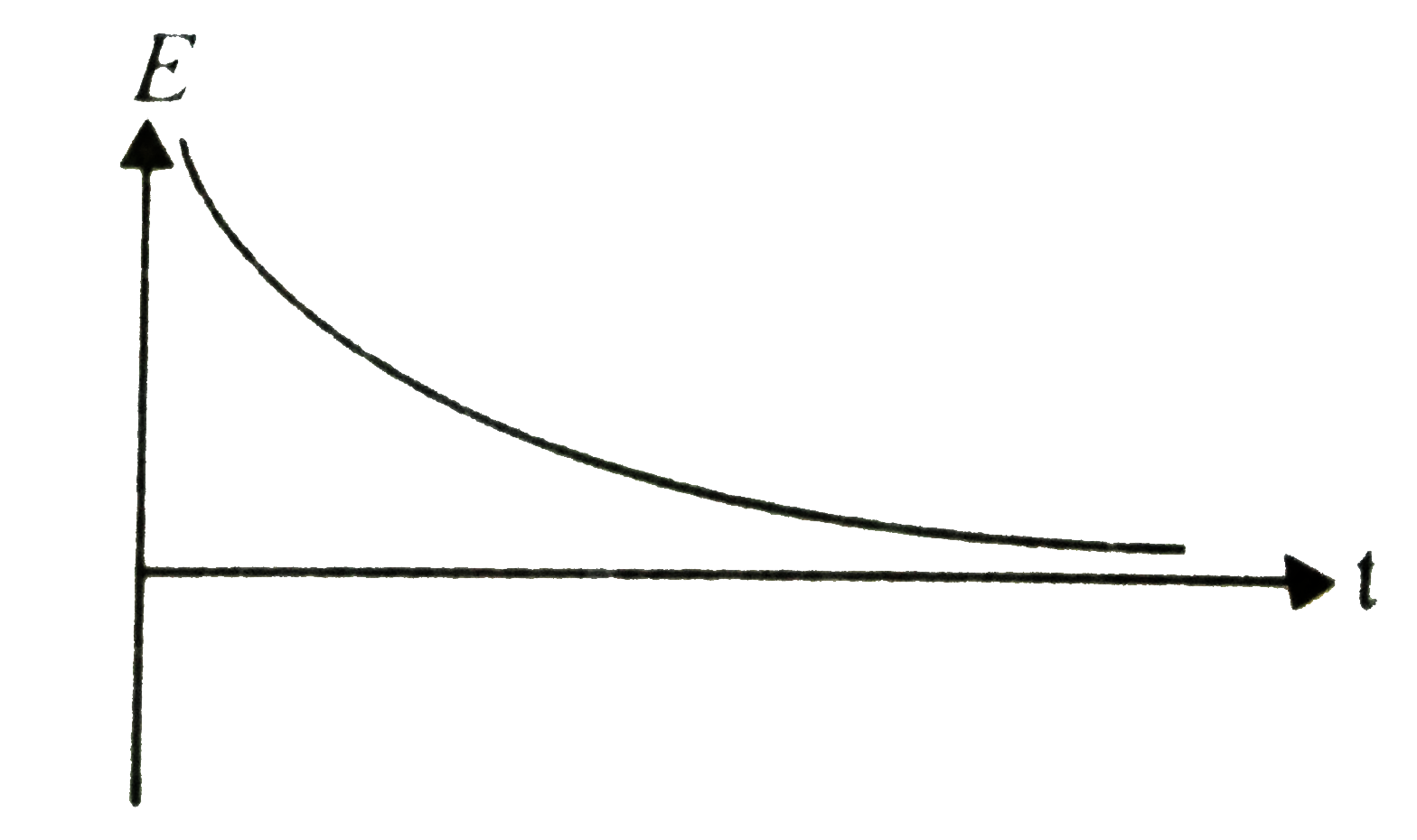 D
D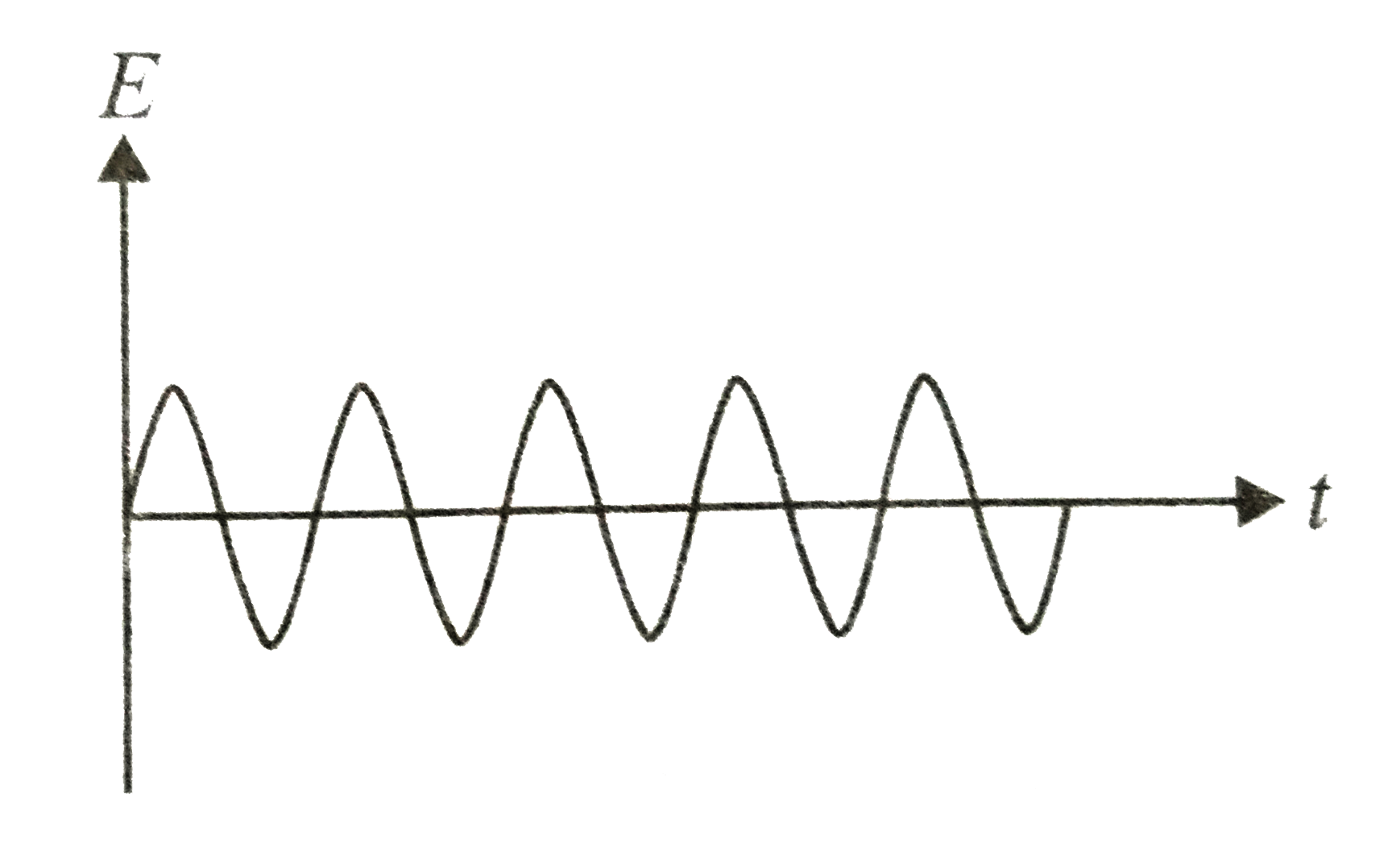
Which one of the following equations of motion represents simple harmonic motion ?
View SolutionWhich of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) The rotation of earth about its axis. (b) Motion of an oscillating mercury column in a U tube,
(c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most position. (d) General vibrations of a polyatomic molecule about its equilibrium position.
View SolutionIn a simple harmonic motion
View SolutionWhich of the following equation represents damped oscillation?
View SolutionDefine simple harmonic motion ?
View Solution
