Two parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is
1.5N/C
1.5×10−10N/C
3.N/C
3×10−6N/C
The correct Answer is:C
To solve the problem of finding the electric field between two parallel large thin metal sheets with equal surface charge densities of opposite signs, we can follow these steps:
1. Understanding the Setup:
- We have two parallel sheets: one with a positive surface charge density σ=26.4×10−12C/m2 and the other with a negative surface charge density −σ.
- The electric field produced by a single infinite sheet of charge is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
2. Calculating the Electric Field Due to Each Sheet:
- For the positively charged sheet, the electric field E+ is directed away from the sheet:
E+=σ2ϵ0
- For the negatively charged sheet, the electric field E− is directed towards the sheet:
E−=−σ2ϵ0
- However, since we are interested in the region between the sheets, both electric fields will add up in that region.
3. Total Electric Field Between the Sheets:
- The total electric field E between the sheets is the sum of the magnitudes of the electric fields due to both sheets:
E=E++|E−|=σ2ϵ0+σ2ϵ0=σϵ0
4. Substituting the Values:
- Now, substituting the value of σ and ϵ0:
E=26.4×10−128.85×10−12
5. Calculating the Electric Field:
- Performing the division:
E≈2.99N/C≈3N/C
6. Final Result:
- The electric field between the two sheets is approximately 3N/C.
- We have two parallel sheets: one with a positive surface charge density σ=26.4×10−12C/m2 and the other with a negative surface charge density −σ.
- The electric field produced by a single infinite sheet of charge is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
- For the positively charged sheet, the electric field E+ is directed away from the sheet:
E+=σ2ϵ0
- For the negatively charged sheet, the electric field E− is directed towards the sheet:
E−=−σ2ϵ0
- However, since we are interested in the region between the sheets, both electric fields will add up in that region.
- The total electric field E between the sheets is the sum of the magnitudes of the electric fields due to both sheets:
E=E++|E−|=σ2ϵ0+σ2ϵ0=σϵ0
- Now, substituting the value of σ and ϵ0:
E=26.4×10−128.85×10−12
- Performing the division:
E≈2.99N/C≈3N/C
- The electric field between the two sheets is approximately 3N/C.
Similar Questions
Two large thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and magnitude 27×10−22Cm−2. The electric field →E in region II in between the plates is

View SolutionAn infinite thin plane sheet of charge density 7.08×10−11(C/m2) is held in air. Find the electric field at a point very close to the sheet.
View Solution
Knowledge Check
Two large, thin plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 16×10−22Cm−2. The electric field between the plates is
A1.8×10−10NC−1B1.9×10−10NC−1C1.6×10−10NC−1D1.5×10−10NC−1Two infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities σ. Electric field at a point between the sheets is
Aσ2ε0Bσε0CzeroDdepends on the location of the point
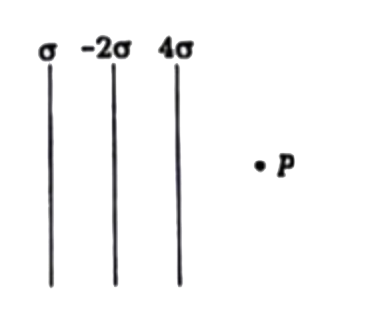
Three non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
View SolutionTwo paralle plane sheets 1 and 2 carry uniform charge densites σ1andσ2 (see fig. The electric field in the region marked I is (σ1>σ2):

View SolutionA large plane charge sheet having surface xharge density σ=2.0×10−6Cm−2 lies in the x-y plane. Find the flux of the electric field through a circular area of radius 1 cm lying completely in the region where x, y, z are all positive and with its normal making an angle of 600 with the z-axis.
View SolutionTwo large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0×10−22C/m2. What is E : between the plates?
View SolutionTwo large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0×10−22C/m2. What is E : between the plates?
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View Solution
