Five capacitors, each of capacitance value C are connecteed as shown in the figure. The ratio of capacitance between P and R, and the capacitance between P and Q, is.
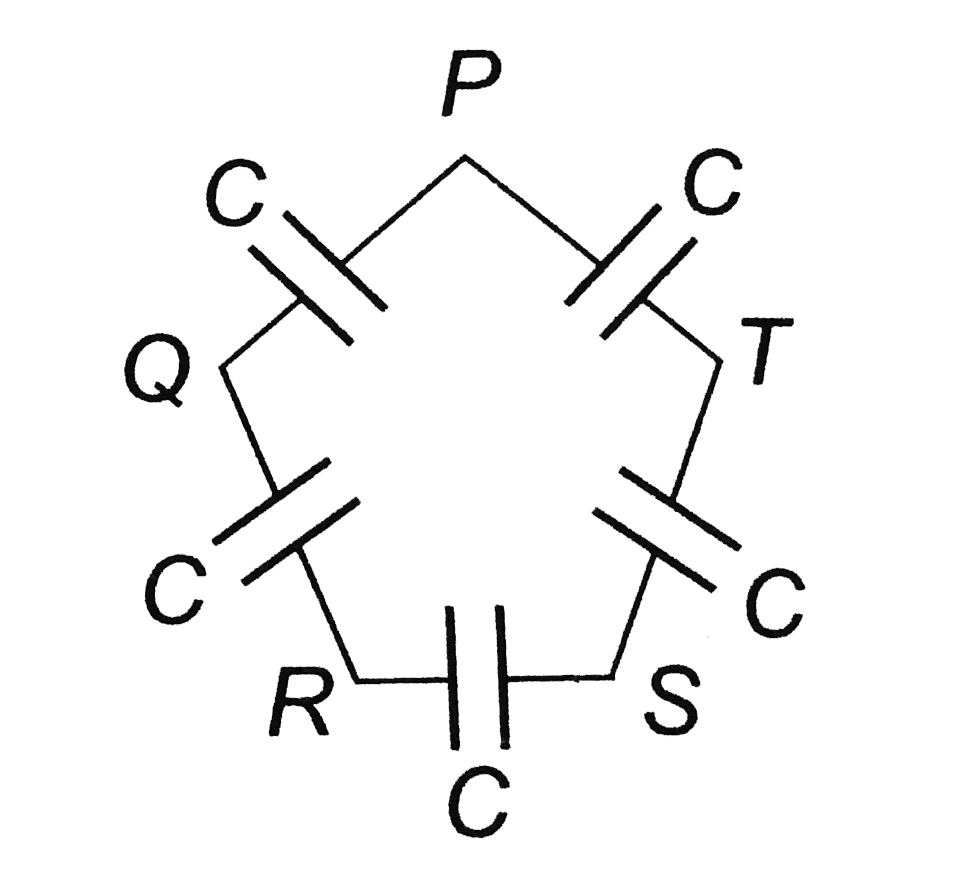
3:1
5:2
2:3
1:1
The correct Answer is:C
Between the points P and Q , a capacitor C1 and series combination of C2,C3,C4,C5 are connected in parallel.
∴1Cs=1C2+1C2+1C4+1C5
=1c+1c+1c+1c=4c
or Cs=C/4
The equivalent capacitance betwen P and Q is C'=C1+C1=C+C4=5C4
Betwen the points P and R a series combination of C1,C2 and a series combination of C3,C4,C5 are connected in parallel.
∴1Cs=1C1+1C2=1C+1Cor,C'=C2
1Cns=1C3+1C4+1C5=1C+1C+1C=3Cor,C''C3
The equivqlent capacitance between P and R is C=Cs+Cs=C2+C3=5C6
∴C''C''=(5C/6)(5C/4)=46=23
Similar Questions
Five capacitors each of capacitance value C are connected as shown in the figure . The ratio of capacitance between P and R and the capacitance between P and Q is
 View Solution
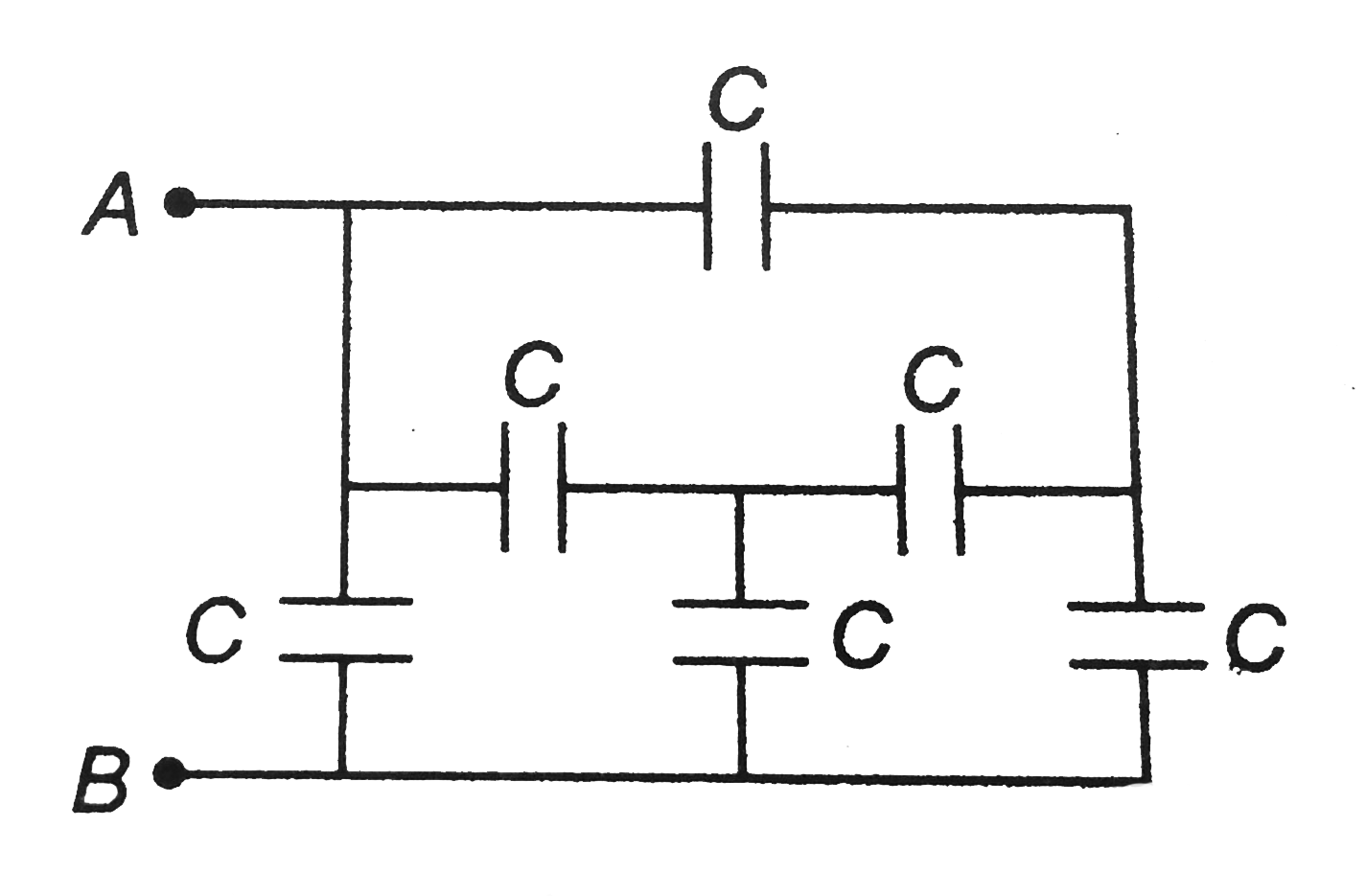
View SolutionSix equal capacitors each of capacitance C are connected as shown in the figure. The equivalent capacitance between points A and B is
 View Solution
View SolutionSix equal capacitors each of capacitance 10μF are connect as shown in the figure. Then the equivalent capacitance between A and B is
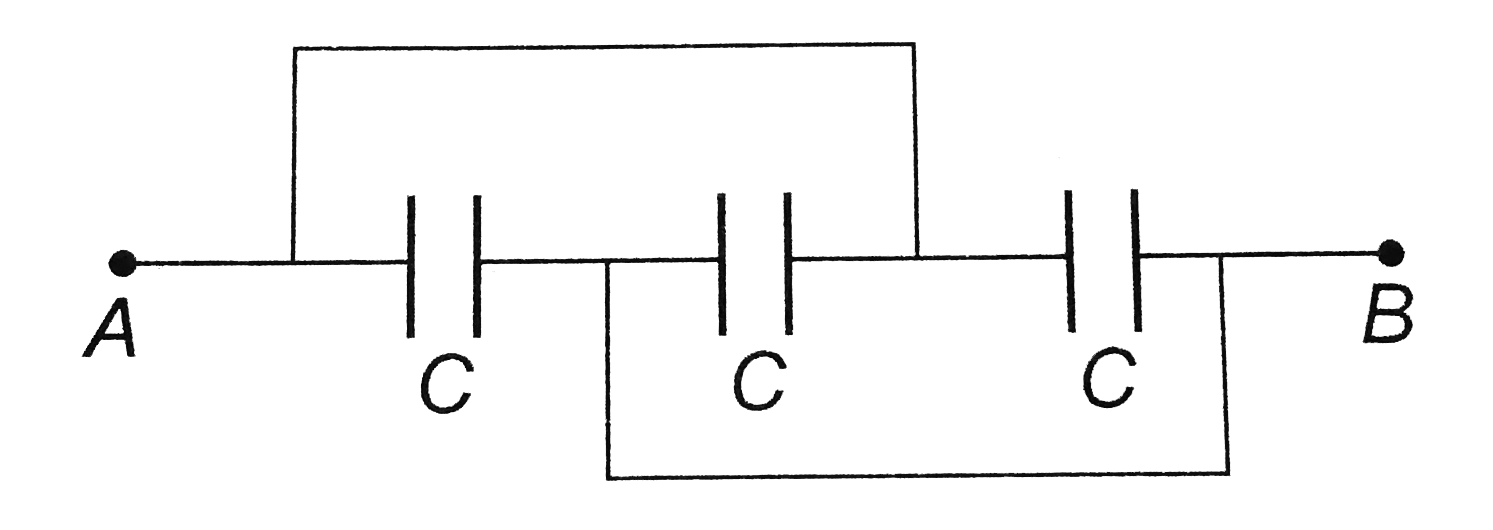
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
 View Solution
View SolutionFour capacitors are connected as shown in the figure. The equivalent capacitance between P and Q is
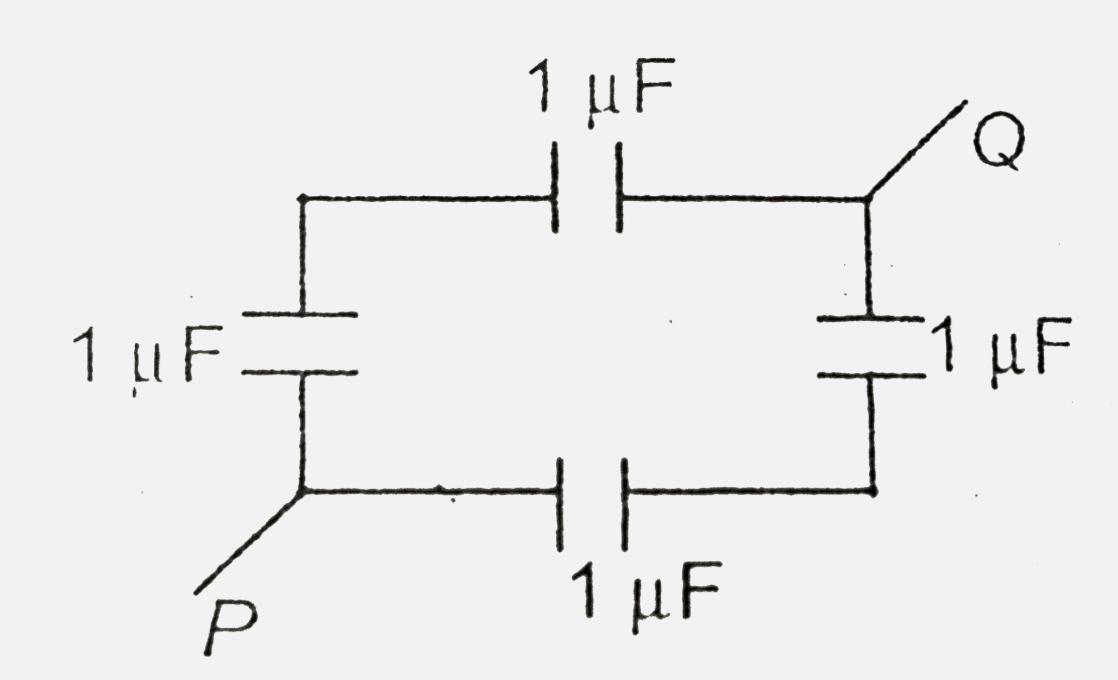 View Solution
View SolutionFour capacitors of each of capacity 3μF are connected as shown in the adjoining figure. The ratio of equivalent capacitance between A and B and between A and C will be
 View Solution
View SolutionIn the circuit as shown in the figure the effective capacitance between A and B is
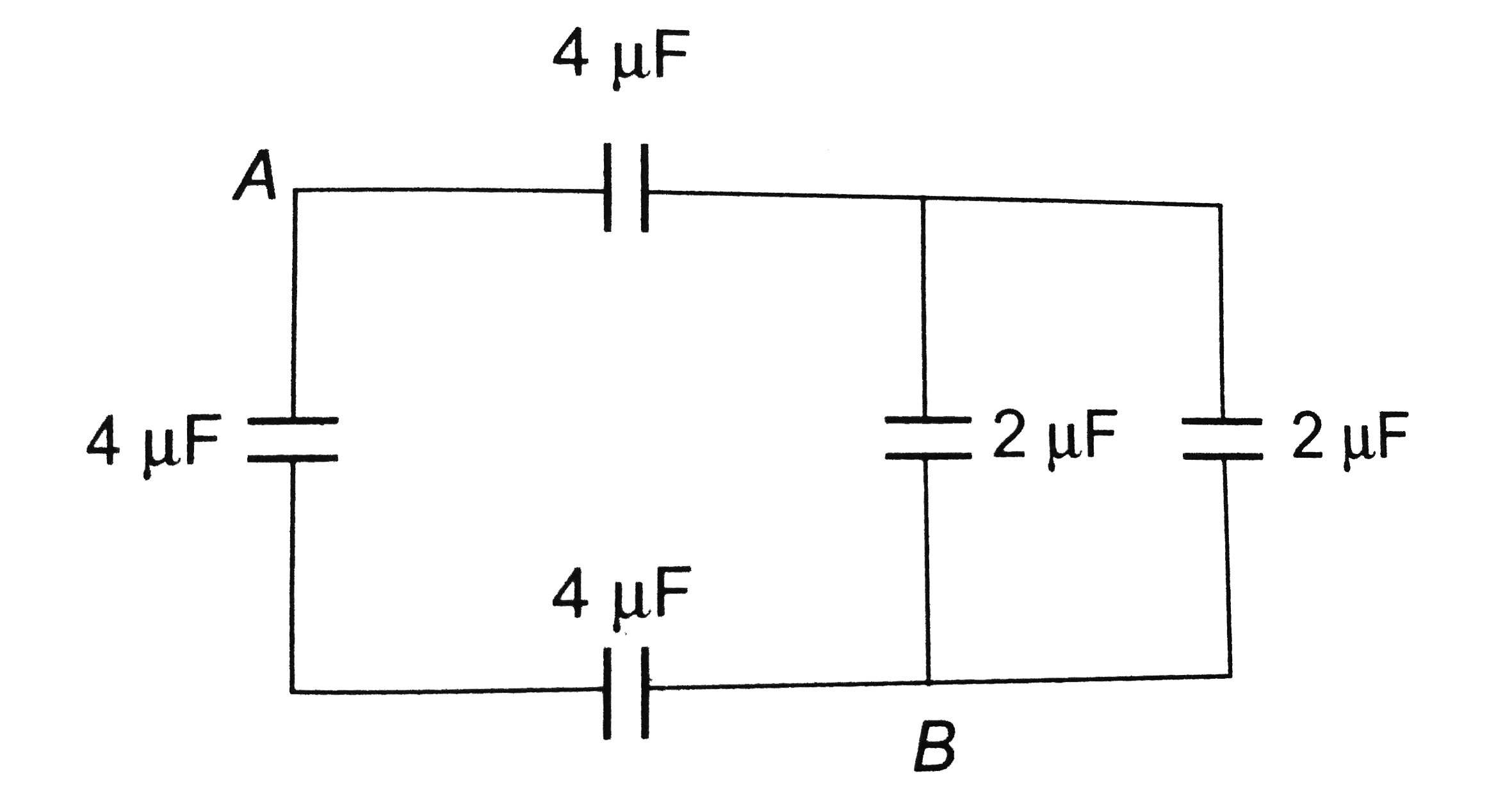 View Solution
View SolutionIn the circuit as shown in the figure the effective capacitance between A and B is
 View Solution
View SolutionSome capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
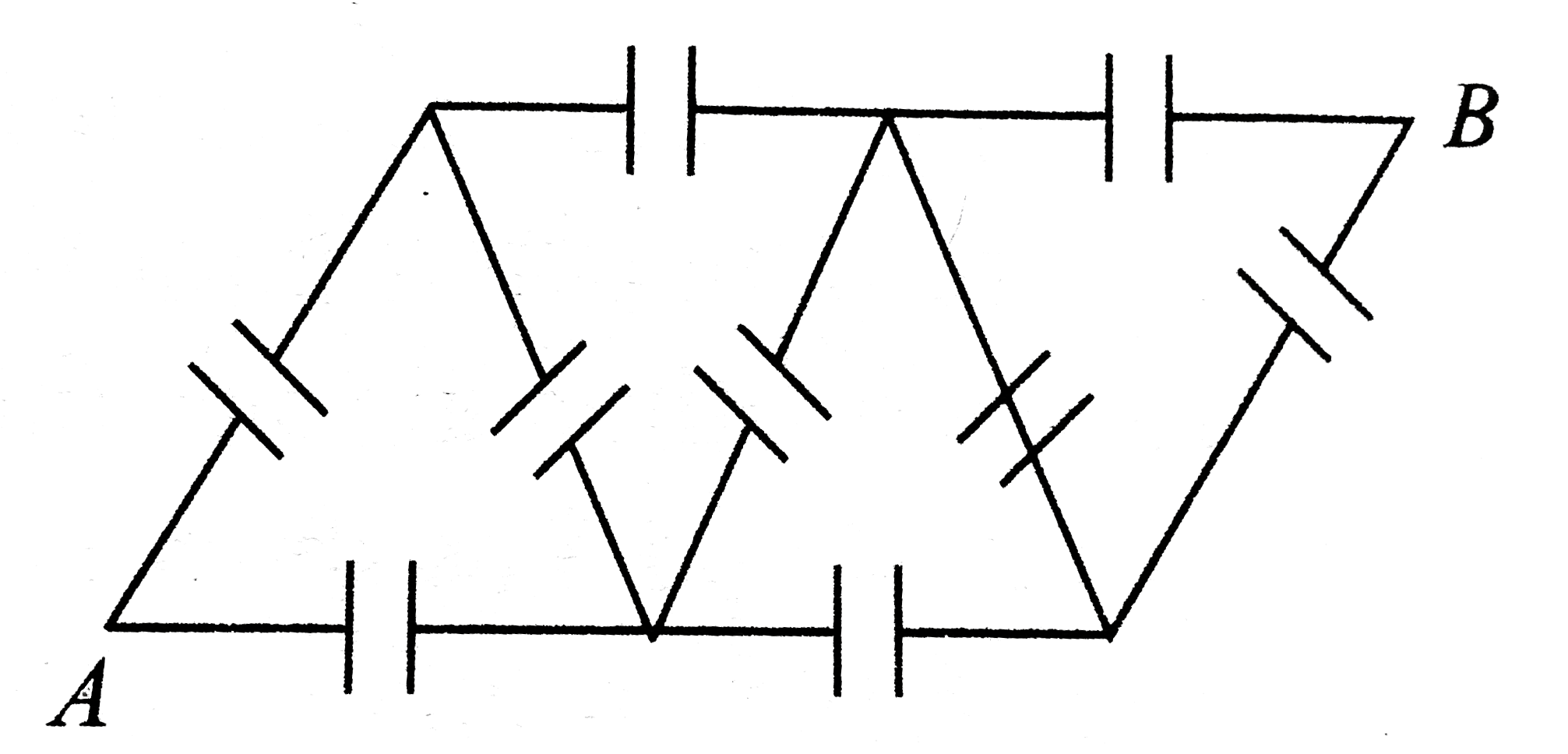 .View Solution
.View SolutionSix identical capacitors each of capacitance 2μF are connected as shown below. The equivalent capacitance between the points A and B is
View Solution



