A strone thrown into still water, creates a circular wave pattern moving radially outwards. If r is the distance measured from the centre of the pattern. The amplitudeof the waves varies as
r−1/2
r−1
r−2
r3/2
The correct Answer is:A
To solve the problem, we need to determine how the amplitude of the waves varies with the distance r from the center of the circular wave pattern created by a stone thrown into still water.
1. Understanding the Wave Pattern:
- When a stone is thrown into still water, it creates circular waves that move outward from the point of impact. The center of the wave pattern is where the stone was thrown.
2. Defining the Variables:
- Let r be the distance from the center of the wave pattern.
- The amplitude of the waves decreases as we move away from the center.
3. Relationship Between Intensity and Distance:
- The intensity I of the wave is inversely proportional to the distance r from the center. This can be expressed mathematically as:
I∝1r
- This means:
I=k⋅1r
where k is a constant.
4. Relationship Between Amplitude and Intensity:
- The amplitude A of a wave is related to the intensity by the formula:
A∝√I
- Substituting the expression for intensity into this equation gives:
A∝√(k⋅1r)=√k⋅1√r
5. Final Expression for Amplitude:
- Therefore, we can express the amplitude as:
A∝1√r
- This can also be written as:
A∝r−12
6. Conclusion:
- The amplitude of the waves varies with the distance r from the center as:
A∝r−12
- Thus, the correct answer is that the amplitude varies as r−12.
- When a stone is thrown into still water, it creates circular waves that move outward from the point of impact. The center of the wave pattern is where the stone was thrown.
- Let r be the distance from the center of the wave pattern.
- The amplitude of the waves decreases as we move away from the center.
- The intensity I of the wave is inversely proportional to the distance r from the center. This can be expressed mathematically as:
I∝1r
- This means:
I=k⋅1r
where k is a constant.
- The amplitude A of a wave is related to the intensity by the formula:
A∝√I
- Substituting the expression for intensity into this equation gives:
A∝√(k⋅1r)=√k⋅1√r
- Therefore, we can express the amplitude as:
A∝1√r
- This can also be written as:
A∝r−12
- The amplitude of the waves varies with the distance r from the center as:
A∝r−12
- Thus, the correct answer is that the amplitude varies as r−12.
Similar Questions
In a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity is
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
If the total energy of the particle is E=−3B216A, and it is known that the motion is radial only then the velocity is zero at
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium distance is given by
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The equilibrium is
View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA star like the sun has serveral bodies moving around it at different distance. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be υ, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum L. As the radius r of the orbit increase, determine which of the above quantities increase and which ones decrease.
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionIn a young's doule slits experiment, a monochromatic source of wavelength λ is used to illuminate the two slits
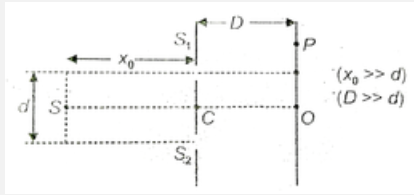
S1 and S2. The slitss S1 and S2 are identical and source S is placed symmetrically as shown. interference pattern is observed on a screen at a distance D from the centre of slit. The distance between the slits is d.
If the source is moved up by a very small distance y0, the central maxima will shift
View Solutiona circular ring carries a chargeQ1 the variation of electric field with distance x measured from centre along Axis for x>>R can be given as (R radius of ring)
View Solution
