Which of the following diagrams represent the veriation of electric field vector with time for a circularly polarised light




The correct Answer is:B
To solve the question regarding which diagram represents the variation of the electric field vector with time for circularly polarized light, we can follow these steps:
Step 1: Understand Circularly Polarized Light
Circularly polarized light consists of two perpendicular electric field components that are out of phase by 90 degrees (or π/2 radians). These components can be represented as:
- Ex=E0sin(ωt)
- Ey=E0sin(ωt+π2)
Step 2: Express the Second Component
Using the trigonometric identity, we can express the second component Ey:
- Ey=E0sin(ωt+π2)=E0cos(ωt)
Step 3: Determine the Resultant Electric Field
The resultant electric field vector can be expressed as:
- →E=Ex^i+Ey^j
Substituting the expressions we have:
- →E=E0sin(ωt)^i+E0cos(ωt)^j
Step 4: Calculate the Magnitude of the Electric Field
The magnitude of the electric field can be calculated as:
- |→E|=√E2x+E2y
Substituting the expressions for Ex and Ey:
- |→E|=√(E0sin(ωt))2+(E0cos(ωt))2
- |→E|=E0√sin2(ωt)+cos2(ωt)
Step 5: Simplify the Magnitude
Using the Pythagorean identity sin2(θ)+cos2(θ)=1:
- |→E|=E0
Step 6: Conclusion
The magnitude of the electric field remains constant over time, which indicates that the electric field vector rotates in a circular motion in the plane perpendicular to the direction of propagation of the light. Thus, the correct diagram representing this behavior will show a constant magnitude with a rotating direction.
Final Answer
Based on the analysis, the correct option is Option A, which represents the constant magnitude of the electric field vector with time for circularly polarized light.
---
Circularly polarized light consists of two perpendicular electric field components that are out of phase by 90 degrees (or π/2 radians). These components can be represented as:
- Ex=E0sin(ωt)
- Ey=E0sin(ωt+π2)
Using the trigonometric identity, we can express the second component Ey:
- Ey=E0sin(ωt+π2)=E0cos(ωt)
The resultant electric field vector can be expressed as:
- →E=Ex^i+Ey^j
Substituting the expressions we have:
- →E=E0sin(ωt)^i+E0cos(ωt)^j
The magnitude of the electric field can be calculated as:
- |→E|=√E2x+E2y
Substituting the expressions for Ex and Ey:
- |→E|=√(E0sin(ωt))2+(E0cos(ωt))2
- |→E|=E0√sin2(ωt)+cos2(ωt)
Using the Pythagorean identity sin2(θ)+cos2(θ)=1:
- |→E|=E0
The magnitude of the electric field remains constant over time, which indicates that the electric field vector rotates in a circular motion in the plane perpendicular to the direction of propagation of the light. Thus, the correct diagram representing this behavior will show a constant magnitude with a rotating direction.
Based on the analysis, the correct option is Option A, which represents the constant magnitude of the electric field vector with time for circularly polarized light.
Similar Questions
Knowledge Check
Which of the following P-V diagram represent the graph of isometric process?
A B
B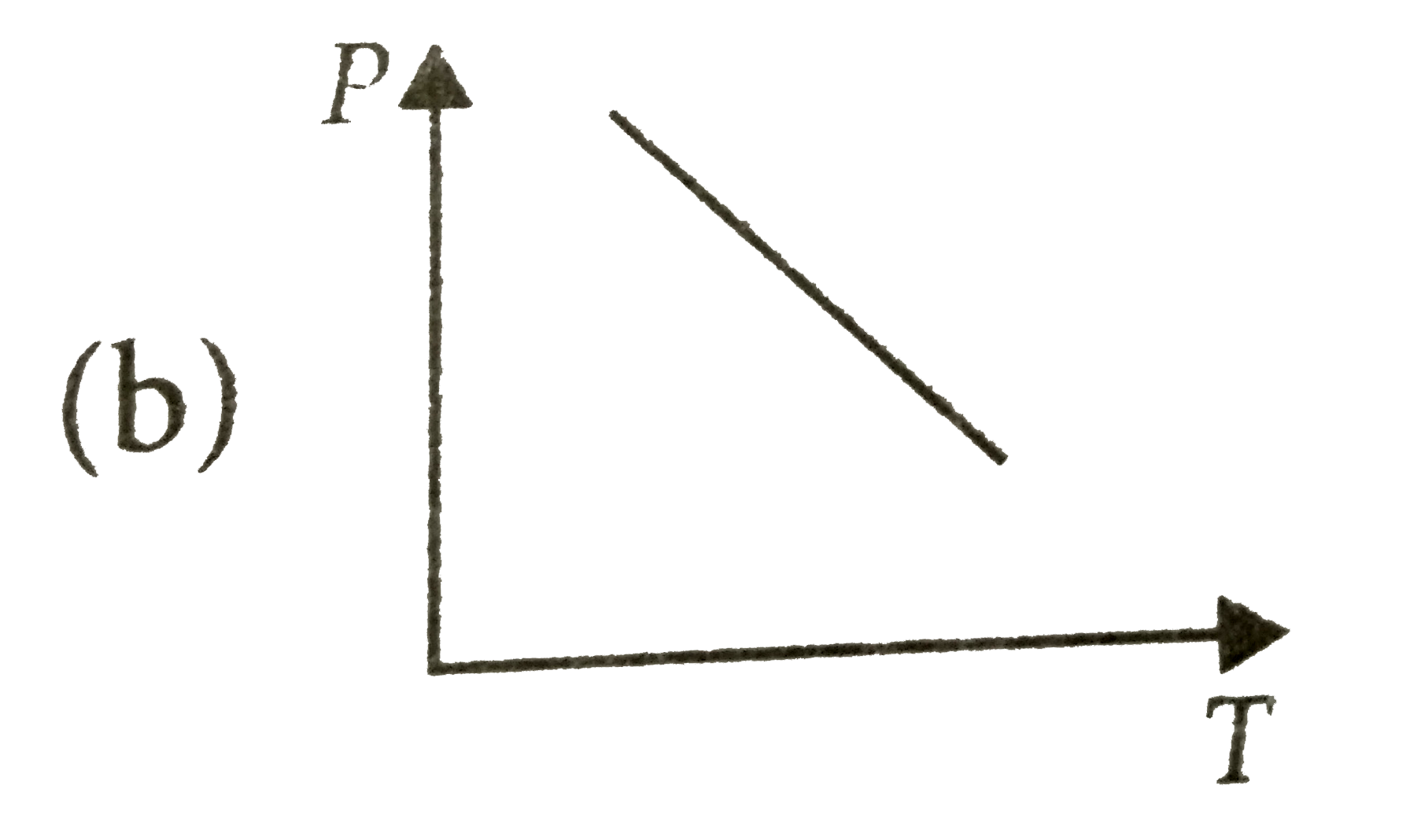 C
C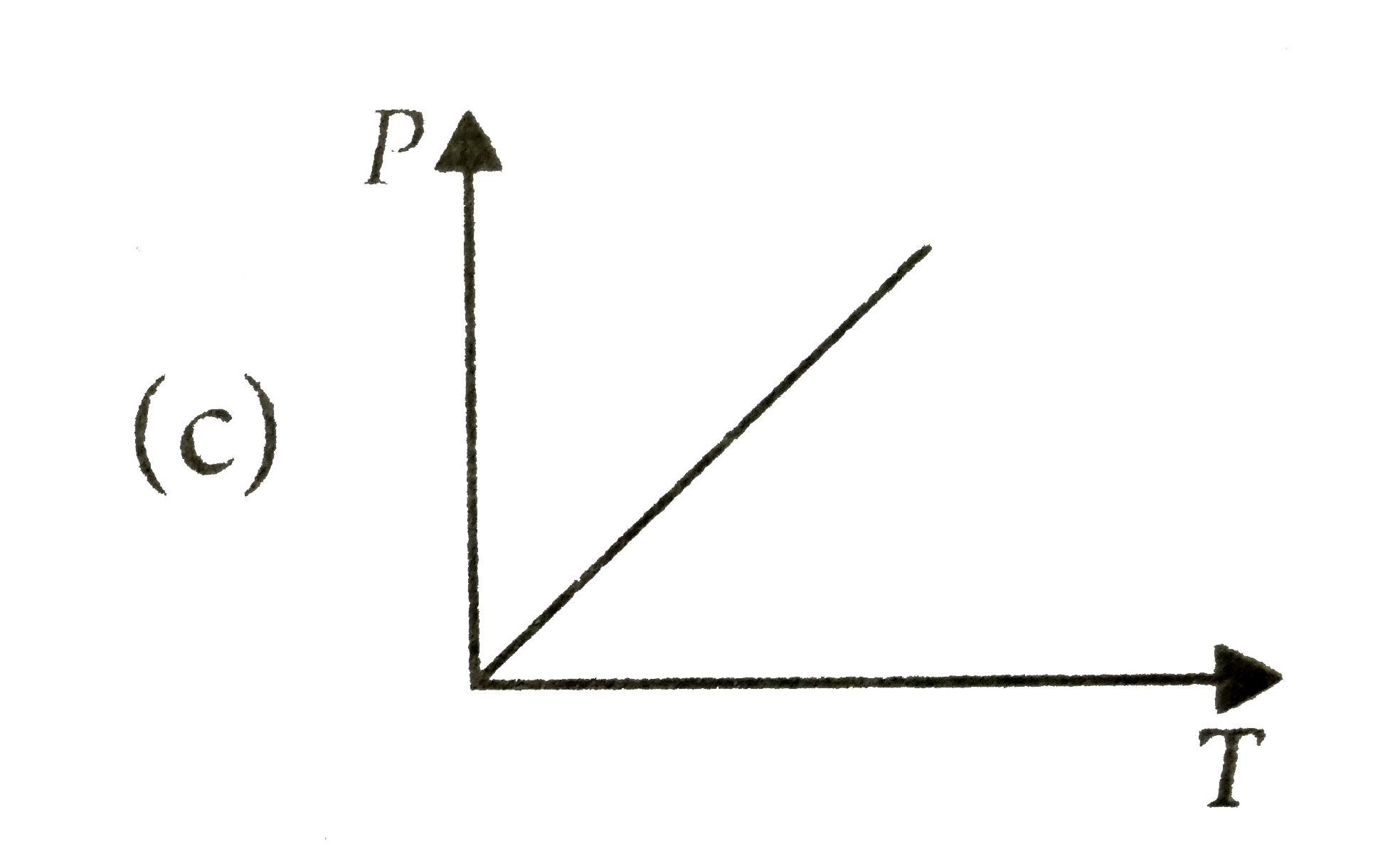 D
D
Which energy diagram best represents the given reaction ?
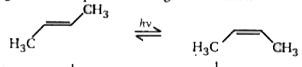 A
A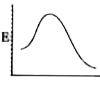 B
B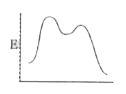 C
C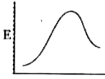 D
D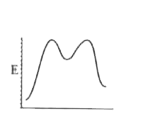
Which of the following arrow diagrams represents a function from Xto Y?
A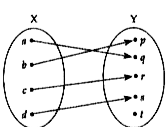 B
B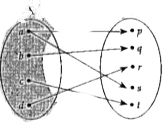 C
C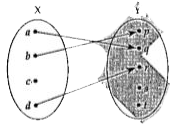 D
D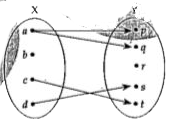
Which of the following Venn diagram represent (A−B)?
View SolutionWhich of the following represents a unit vector ?
View SolutionWhich of the following represents a vector ?
View SolutionWhich one of the following diagrams represents the placentation in Dianthus
View SolutionWhich one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View Solution