The camera lens has an aperture of f and the exposure time is (1/60)s. What will be the new exposure time if the aperture become 1.4f ?
142
156
172
131
The correct Answer is:D
To solve the problem, we need to understand the relationship between the exposure time (T) and the aperture size (f). The exposure time is directly proportional to the square of the aperture size.
1. Identify the relationship:
The exposure time (T) is directly proportional to the square of the aperture (f). This can be expressed mathematically as:
T∝f2
or
T1f21=T2f22
2. Assign known values:
From the problem, we know:
- Initial exposure time, T1=160 seconds
- Initial aperture, f1=f
- New aperture, f2=1.4f
3. Set up the equation:
Substitute the known values into the equation:
1/60f2=T2(1.4f)2
4. Simplify the equation:
We can simplify (1.4f)2:
(1.4f)2=1.96f2
Now, substituting this back into the equation gives:
1/60f2=T21.96f2
5. Cancel out f2:
Since f2 is common in both the numerator and denominator, we can cancel it:
160=T21.96
6. Solve for T2:
Rearranging the equation to solve for T2:
T2=160×1.96
T2=1.9660
7. Convert to a simpler fraction:
To simplify 1.9660:
T2=1966000=983000≈130
8. Final answer:
Therefore, the new exposure time T2 is approximately:
T2≈130 seconds
The exposure time (T) is directly proportional to the square of the aperture (f). This can be expressed mathematically as:
T∝f2
or
T1f21=T2f22
From the problem, we know:
- Initial exposure time, T1=160 seconds
- Initial aperture, f1=f
- New aperture, f2=1.4f
Substitute the known values into the equation:
1/60f2=T2(1.4f)2
We can simplify (1.4f)2:
(1.4f)2=1.96f2
Now, substituting this back into the equation gives:
1/60f2=T21.96f2
Since f2 is common in both the numerator and denominator, we can cancel it:
160=T21.96
Rearranging the equation to solve for T2:
T2=160×1.96
T2=1.9660
To simplify 1.9660:
T2=1966000=983000≈130
Therefore, the new exposure time T2 is approximately:
T2≈130 seconds
Similar Questions
With diaphragm of the camera lens set at f2 , the correct exposure time is 1100 , then with diaphragm set at f4. Calculate the correct exposure time.
View SolutionA camera objective has an aperture diameter d . If the aperture is reduced to diameter d/2 the exposure time under identical conditions of light should be made
View SolutionThe time period of a satellite of earth is 5 hours. If the separation between the centre of earth and the satellite is increased to 4 times the previous value, the new time period will become-
View SolutionThe time period of a satellite of earth is 5 hours. If the separation between the centre of earth and the satellite is increased to 4 times the previous value, the new time period will become-
View SolutionA thin lens focal length f and its aperture has diameter d. It forms an image of intensity I. Now the central part of the aperture up to diameterd2 is blocked by an opaque paper. The focal length and image intensity will change to
View SolutionA parallel beam of light falls on the surface of a convex lens whose radius of curvature of both sides of 20cm. The refractive index of the material of the lens varies as μ=1.5+0.5r , where r is the distance of the point on the aperture from the optical centre in cm. Find the length of the region on the axis of the lens where the light will appear. The radius of aperture of the lens is 1cm.
View SolutionA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
View SolutionIn a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength 6000Å and intensity (10/π) W m−2 is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness 2000Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
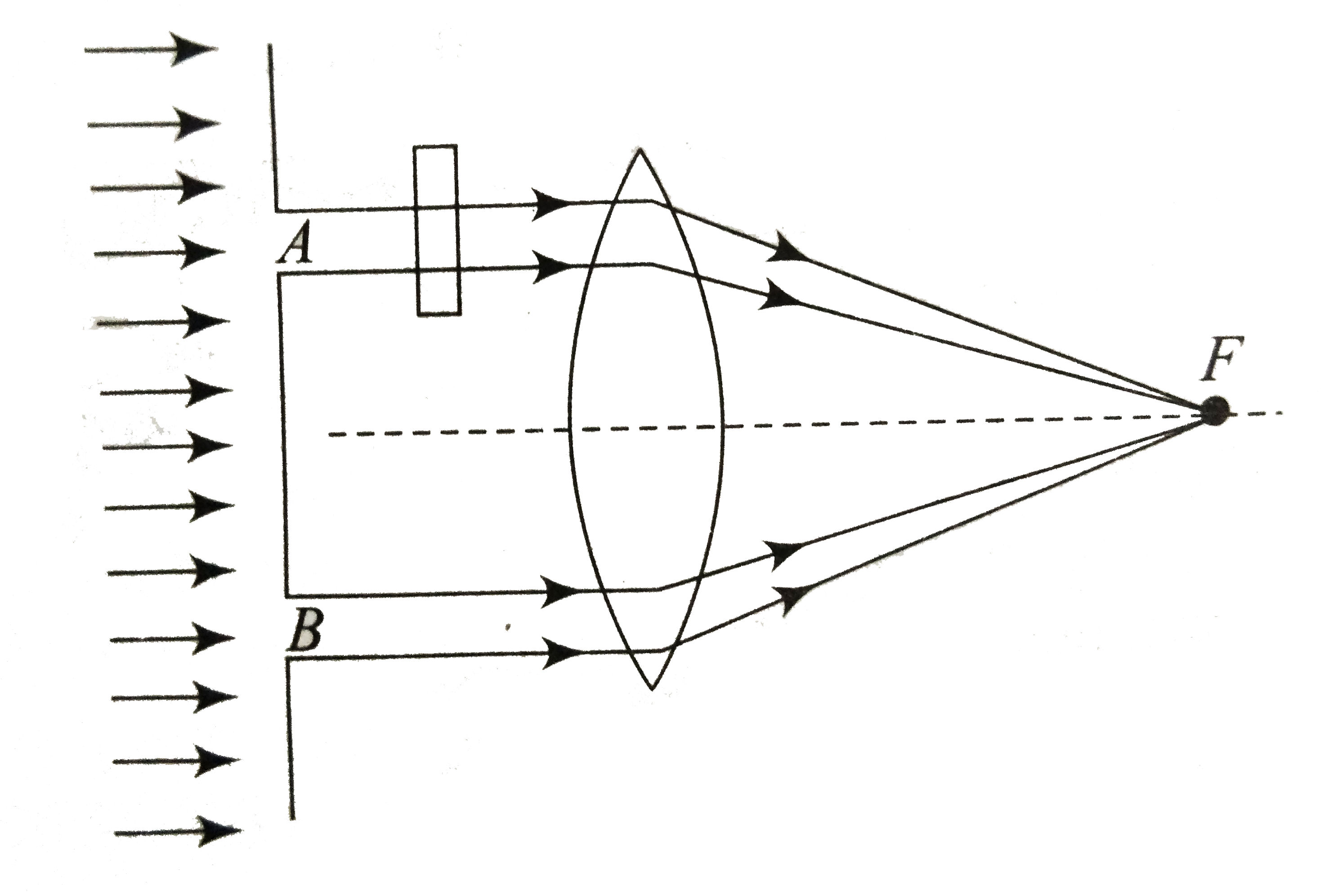
View SolutionDiameter or aperture of a plano - convex lens is 6 cm and its thickness at the centre is 3 mm. The image of an object formed is real and twice the size of the object. If the speed of light in the material of the lens is 2×108ms−1. The distance where the object is placed from the plano - convex lens is .............. ×15cm.
View SolutionAn object is kept at rest on the principal axis of a lens. Initially the object is at a distance three times the focal length 'f' of the lens. The lens runs towards the object at a constant speed u, until the distance between the object and its real image becomes 4f. If the iamge always forms on a moving screen then express the velocity of the screen as a function of time.
View Solution
