A point source is kept at a distance of 1000 m has an illumination I. To change the illumination to 16I the new distance should become
a.250 m
b.500 m
c.750 m
d.800 m
The correct Answer is:A
To solve the problem, we need to understand the relationship between illumination (I) and distance (R) from a point source. The illumination (I) from a point source is inversely proportional to the square of the distance (R) from the source. This can be expressed mathematically as:
I∝1R2
1. Identify Initial Conditions:
- Let the initial illumination be I1=I.
- The initial distance from the source is R1=1000m.
2. Identify Final Conditions:
- The final illumination is I2=16I.
- We need to find the new distance R2.
3. Set Up the Proportionality Relationship:
- From the inverse square law of illumination, we can write:
I1I2=R22R21
4. Substitute Known Values:
- Substitute I1=I and I2=16I:
I16I=R22(1000)2
- This simplifies to:
116=R2210002
5. Cross Multiply to Solve for R22:
R22=1000216
6. Calculate R22:
- Calculate 10002=1000000:
R22=100000016=62500
7. Find R2:
- Take the square root of both sides:
R2=√62500=250m
Final Answer:
The new distance R2 should be 250 m.
---
- Let the initial illumination be I1=I.
- The initial distance from the source is R1=1000m.
- The final illumination is I2=16I.
- We need to find the new distance R2.
- From the inverse square law of illumination, we can write:
I1I2=R22R21
- Substitute I1=I and I2=16I:
I16I=R22(1000)2
- This simplifies to:
116=R2210002
R22=1000216
- Calculate 10002=1000000:
R22=100000016=62500
- Take the square root of both sides:
R2=√62500=250m
The new distance R2 should be 250 m.
Similar Questions
A point source of light is kept at a distance of 15cm from a converging lens,on its optical axis.The focal length of the lens is 10cm and its diameter is 3cm ,A screen is placed on the other side of the lens ,perpendicular to the axis of lens,at a distance 20cm from it.Then find the area of the illuminated part of the screen?
View SolutionThe intensity of sound from a point source is 1.0×10−8Wm−2, at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source ?
View SolutionIf two identical spheres having charge 16μC and −8μC are kept at certain distance apart , then the force if F. They are touched and again kept at the same distance , the force becomes.
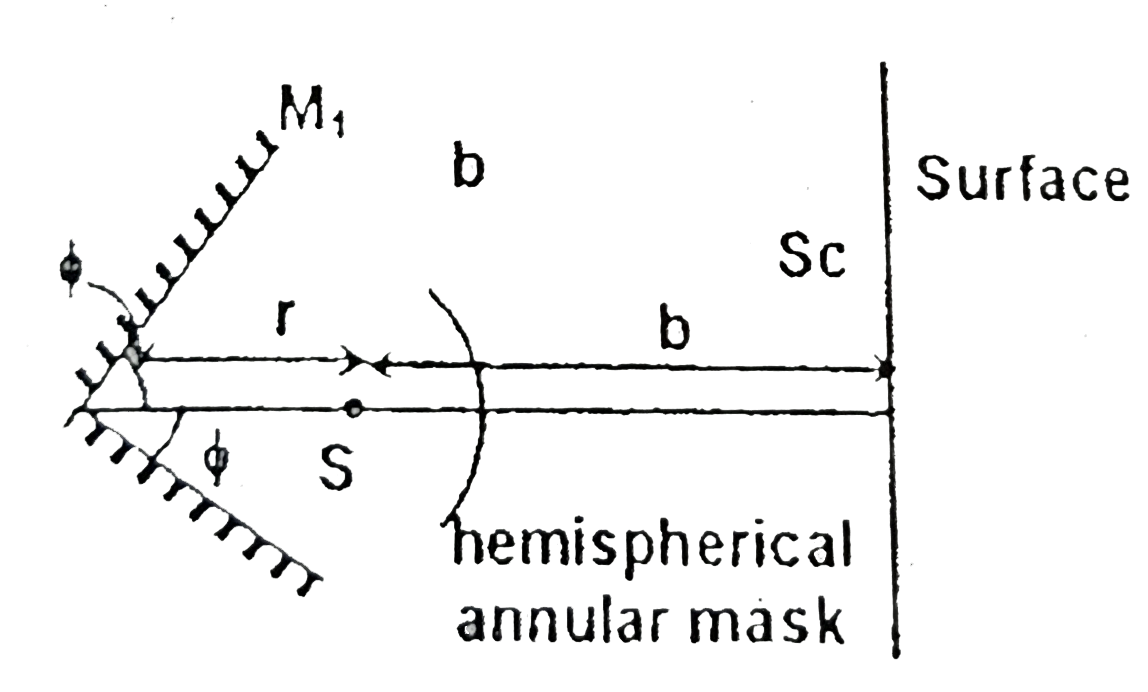
View SolutionTwo mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionWhen a point source of light is at a distance of 50 cm from a photoelectric cell , the cut-off voltage is found to be V0 . If the same source is placed at a distance of 1 m from the cell , then the cut-off voltage will be
View SolutionA point source O kept at distance of 2R from pole P of concave interface having radius of curvature R emits a unidirectional beam at an angle of 30∘ to the principal axis PO. The distance of the image of point source O from pole P is

View SolutionA point object is kept at a distance of 2 m from a parabolic reflecting surface y2=2x . An equiconvex lens is kept at a distance of 1.80 m from the parabolic surface. The focal length of the lens is 20 cm . Find the position from origin of the image in cm, after reflection from the surface.
_S01_032_Q01.png)
View SolutionIn Young.s double slit experiment, the screen is kept at a distance of 1.2m from the plane of the slits. The two slits are separated by 5mm and illuminated with monochromatic light having wavelength 600 mm. Calculate:
Frings width i.e., fringe separation of the interference pattern.
View SolutionTwo slits are separated by a distance of 0.5mm and illuminated with light of λ=6000Å. If the screen is placed 2.5m from the slits. The distance of the third bright image from the centre will be
View Solution
