Black holes in orbit around a normal star are detected from the earth due to the fricitional heating of infalling gas into the black hole, which can reach temperature greater than 106K. Assuming that the infalling gas can be modelled as a blackbody radiator, then the wavelenght of maximum power lies
in the visible region
in the X-ray region
in the microwave region
in the gamma-ray region of electromagnetic spectruem
The correct Answer is:B
To solve the problem of determining the wavelength of maximum power emitted by the infalling gas into a black hole, we will use the principles of blackbody radiation and Wien's displacement law.
1. Understanding the Problem:
We know that the infalling gas can be modeled as a blackbody radiator at a temperature T greater than 106 K. We need to find the wavelength at which the maximum power is emitted.
2. Using Wien's Displacement Law:
Wien's displacement law states that the wavelength λmax at which the emission of a blackbody spectrum is maximized is inversely proportional to the temperature T:
λmax=bT
where b is Wien's displacement constant, approximately 2.898×10−3m K.
3. Substituting the Temperature:
Given T>106K, we can use this value to find λmax:
λmax=2.898×10−3106
4. Calculating λmax:
Performing the calculation:
λmax=2.898×10−3106=2.898×10−9m=2.898nm
5. Identifying the Wavelength Range:
The calculated wavelength 2.898nm falls within the X-ray region of the electromagnetic spectrum (which ranges from approximately 0.01nm to 10nm).
6. Conclusion:
Therefore, the wavelength of maximum power emitted by the infalling gas around the black hole lies in the X-ray region.
Final Answer:
The wavelength of maximum power lies in the X-ray region.
---
We know that the infalling gas can be modeled as a blackbody radiator at a temperature T greater than 106 K. We need to find the wavelength at which the maximum power is emitted.
Wien's displacement law states that the wavelength λmax at which the emission of a blackbody spectrum is maximized is inversely proportional to the temperature T:
λmax=bT
where b is Wien's displacement constant, approximately 2.898×10−3m K.
Given T>106K, we can use this value to find λmax:
λmax=2.898×10−3106
Performing the calculation:
λmax=2.898×10−3106=2.898×10−9m=2.898nm
The calculated wavelength 2.898nm falls within the X-ray region of the electromagnetic spectrum (which ranges from approximately 0.01nm to 10nm).
Therefore, the wavelength of maximum power emitted by the infalling gas around the black hole lies in the X-ray region.
The wavelength of maximum power lies in the X-ray region.
Similar Questions
Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load is
View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
If vapours are collected in a container of volume 8.21L maintained at 3T/2K, where T=50K, then the ratio of initial rate of effusion of gases A and B is given as
View Solution
Knowledge Check
This passage is adapted from Geoffrey Giller, “Long a Mystery, How 500-Meter-High Undersea Waves Form Is Revealed.” ©2014 by Scientific American.
nearly impossible to see. Unlike other large waves, these rollers, called internal waves, do not ride the ocean surface. Instead, they move underwater, undetectable without the use of satellite imagery or sophisticated monitoring equipment. Despite their hidden nature, internal waves are fundamental parts of ocean water dynamics, transferring heat to the ocean depths and bringing up cold water from below. And they can reach staggering heights—some as tall as skyscrapers.
Because these waves are involved in ocean mixing and thus the transfer of heat, understanding them is crucial to global climate modeling, says Tom Peacock, a researcher at the Massachusetts Institute of Technology. Most models fail to take internal waves into account. “If we want to have more and more accurate climate models, we have to be able to capture processes such as this,” Peacock says.
Peacock and his colleagues tried to do just that. Their study, published in November in Geophysical Research Letters, focused on internal waves generated in the Luzon Strait, which separates Taiwan and the Philippines. Internal waves in this region, thought to be some of the largest in the world, can reach about 500 meters high. “That’s the same height as the Freedom Tower that’s just been built in New York,” Peacock says.
the South China Sea and beyond, they didn’t know exactly how internal waves formed. To find out, Peacock and a team of researchers from M.I.T. and Woods Hole Oceanographic Institution worked with France’s National Center for Scientific Research using a giant facility there called the Coriolis Platform. The rotating platform, about 15 meters (49.2 feet) in diameter, turns at variable speeds and can simulate Earth’s rotation. It also has walls, which means scientists can fill it with water and create accurate, large-scale simulations of various oceanographic scenarios.
Peacock and his team built a carbon-fiber resin scale model of the Luzon Strait, including the islands and surrounding ocean floor topography. Then they filled the platform with water of varying salinity to replicate the different densities found at the strait, with denser, saltier water below and lighter, less briny water above. Small particles were added to the solution and illuminated with lights from below in order to track how the liquid moved. Finally, they re-created tides using two large plungers to see how the internal waves themselves formed.
The Luzon Strait’s underwater topography, with a distinct double-ridge shape, turns out to be responsible for generating the underwater waves. As the tide rises and falls and water moves through the strait, colder, denser water is pushed up over the ridges into warmer, less dense layers above it.
This action results in bumps of colder water trailed by warmer water that generate an internal wave. As these waves move toward land, they become steeper—much the same way waves at the beach become taller before they hit the shore—until they break on a continental shelf.
The researchers were also able to devise a mathematical model that describes the movement and formation of these waves. Whereas the model is specific to the Luzon Strait, it can still help researchers understand how internal waves are generated in other places around the world.
Eventually, this information will be incorporated into global climate models, making them more accurate. “It’s very clear, within the context of these [global climate] models, that internal waves play a role in driving ocean circulations,” Peacock says.
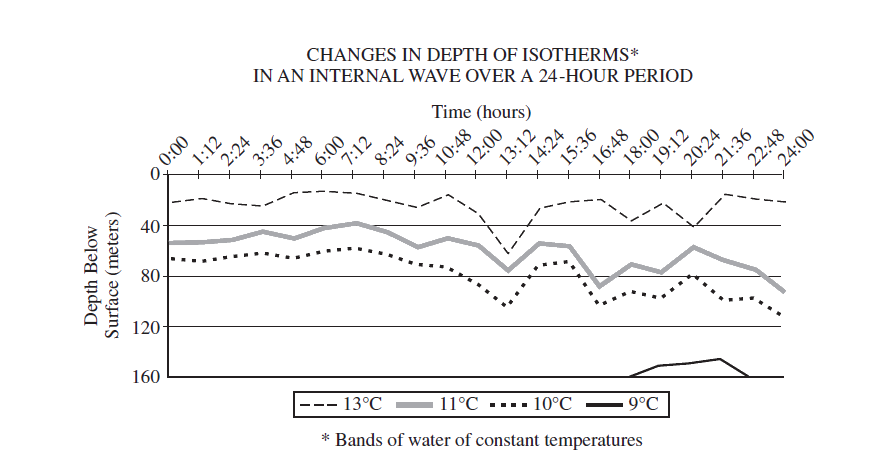
Adapted from Justin Small et al., “Internal Solitons in the Ocean: Prediction from SAR.” ©1998 by Oceanography, Defence Evaluation and Research Agency.
The first paragraph serves mainly toAexplain how a scientific device is used.Bnote a common misconception about an event.Cdescribe a natural phenomenon and address its importance.Dpresent a recent study and summarize its findings.
Scientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
In the core of nucleus fusion reactor , the gas become plasma because of
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
In the core of nucleus fusion reactor , the gas become plasma because of
View SolutionThe system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK. Standard vapour pressures of A and B are P0A and P0B, respectively, at TK. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2TK and second container is maintained at 3T/2. At the temperature greater than TK, both A and B exist in only gaseous form.
We assume than collected gases behave ideally at 2TK and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as:
Ak−−→B, where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

r=K.P√M0
where P= pressure differences between system and surrounding
K= positive constant
M0= molecular weight of the gas
Vapours of A and B are passed into a container of volume 8.21L, maintained at 2TK, where T=50K and after 5min, moles of B=8/3. The pressure developed into the cotainer after two half lives is
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
Result of calculations for four different design of a fusion reactor using D−D reaction are given below. which of these is most promising based on Lawson criterion ?
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
k=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
Assume that two deuteron nuclei in the core of fusion reactor at temperature energy T are moving toward each other, each with kinectic energy 1.5kT , when the seperation between them is large enough to neglect coulomb potential energy . Also neglate any interaction from other particle in the core . The minimum temperature T required for them to reach a separation of 4×10−15m is in the range
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
Assume that two deuteron nuclei in the core of fusion reactor at temperature energy T are moving toward each other, each with kinectic energy 1.5kT , when the seperation between them is large enough to neglect coulomb potential energy . Also neglate any interaction from other particle in the core . The minimum temperature T required for them to reach a separation of 4×10−15m is in the range
View SolutionCloud formation condition
Consider a simplified model of cloub formation. Hot air in contact with the earth's surface contains water vapor. This air rises convectively till the water vapor content reaches its situation pressure. When this happens, the water vpor starts condensing and droplets are formed. We shall estimate the estimate the height a which this happens.We assume that the atmosphere consists of the diatomic gases oxygen and nitrogen in the mass proportion 21:79 respectively. We further assume that the atmosphere is an ideal gas, g the acceleration due to gravity is constant and air processes are adiabatic. Under these assumptions one can show that the pressure is given by
p=p0(T0−TzT0)α
Here p0 and T0 is the pressure and temperature respectively at seal level (z=0),T is the lapse rate (magnitude of the change in temperature T with height z abive the earth's surface, i.e. T>0).
View Solution
