The variation of volume V, with temperature T, keeping pressure constant is called the coefficient of thermal expansion (α) of a gas,
i.e., α=1V(δVδT)P.
For an ideal gas α is equal to
T
1/T
P
1/P
The correct Answer is:B
To find the coefficient of thermal expansion α for an ideal gas, we start with the definition of α:
α=1V(ΔVΔT)P
where V is the volume, T is the temperature, and the subscript P indicates that the pressure is constant.
Step 1: Use the Ideal Gas Law
For an ideal gas, we know that the relationship between pressure P, volume V, and temperature T is given by the ideal gas equation:
PV=nRT
where n is the number of moles and R is the ideal gas constant.
Step 2: Solve for Volume
Rearranging the ideal gas equation to express volume V:
V=nRTP
Step 3: Differentiate Volume with Respect to Temperature
To find ΔV with respect to ΔT at constant pressure, we differentiate V:
ΔVΔT=nRP
Step 4: Substitute into the Expression for α
Now we substitute ΔVΔT back into the equation for α:
α=1V(ΔVΔT)P=1V⋅nRP
Step 5: Substitute V from the Ideal Gas Equation
Now, we substitute V from our earlier expression:
α=1nRTP⋅nRP
Step 6: Simplify the Expression
This simplifies to:
α=PnRT⋅nRP=1T
Conclusion
Thus, for an ideal gas, the coefficient of thermal expansion α is given by:
α=1T
Similar Questions
An ideal gas is expanding such that PT2=constant. The coefficient of volume expansion of the gas is-
View SolutionAn ideal gas is expanding such that PT2=constant. The coefficient of volume expansion of the gas is-
View SolutionCan we related the thermal coefficient of linear expansion, α, to the thermal coefficient of volume expansion?
View SolutionIdeal gas equation is represented as PV=nRT. Gases present in universe were fond ideal in the Boyle's temperature range only and deviated more from ideal gas behavior at high pressure and low temperature.
The deviation are explained in term of compressibility factor z. For ideal behavior Z=PVnRT=1. the main cause to show deviavtion were due to wrong assumptions made about forces oif attractions (which becomes significant at high pressure ) and volume V occupied by molecules in PV=nRT is supposed to be volume of gas or the volume of container in which gas is placed by assuming that gaseous molecules do not have appreciable volume. Actually volume of the gas is that volume in which each molecule of gas can move freely. If volume occupied by gaseous molecule is not negligible, then the term V would be replaced by the ideal volume which by available for free motion of each molecule of gas in 1 mole gas.
Vactual= volume of container -volume occupied by molecules
=v−b
Where b represent the excluded volume occupied by molecules present in one mole of gas.
Similarly for n mole gas
Vactual=v−nb
The ratio of coefficient of thermal expansion α=(∂V∂T)PV and the isothermal compressibility
β=−(∂V(∂P)T) for an ideal gas is:
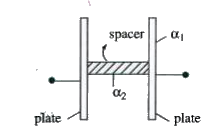
View SolutionA capacitor is to be designed to operate, with constant capacitance, even when temperature varies.The distance between plates is adjusted by spacer to compensate temperature effect. Let α1andα2 be the coefficient of thermal expansion of plate and spacer respectively. Find the ratio of α2α1 . So that no change in capacitance of capacitor with change in temperature.
View SolutionShow that the volume thermal expansion coefficient for an ideal gas at constant pressure is 1T.
View SolutionShow that the volume thermal expansion coefficient for an ideal gas at constant pressure is 1T.
View SolutionShow that the volume thermal expansion coefficient for an ideal gas at constant pressure is 1T.
View SolutionFor an ideal gas PT11 = constant then volume expansion coefficient is equal to :-
View SolutionThe ratio among coefficient of volume expansion, superficial expansion and linear expansion i.e.,
γ : β : α is
View Solution
