In an isobaric process, when temperature changes from is equal to
The correct Answer is:A
To solve the problem of finding the change in entropy (ΔS) during an isobaric process when the temperature changes from T1 to T2, we can follow these steps:
1. Understand the Isobaric Process:
- In an isobaric process, the pressure remains constant. Therefore, we denote the initial and final pressures as P1 and P2, respectively, where P1 = P2.
2. Entropy Change Formula:
- The change in entropy (ΔS) for a process can be expressed as:
ΔS=Cpln(T2T1)−Rln(P2P1)
- Here, Cp is the heat capacity at constant pressure, T1 and T2 are the initial and final temperatures, and R is the universal gas constant.
3. Apply the Isobaric Condition:
- Since the process is isobaric, we have P1=P2. Therefore, the term ln(P2P1) becomes ln(1), which is equal to 0.
4. Simplify the Entropy Change:
- With the above simplification, the equation for ΔS reduces to:
ΔS=Cpln(T2T1)
5. Final Expression:
- Thus, the change in entropy during the isobaric process when the temperature changes from T1 to T2 is given by:
ΔS=Cpln(T2T1)
- In an isobaric process, the pressure remains constant. Therefore, we denote the initial and final pressures as P1 and P2, respectively, where P1 = P2.
- The change in entropy (ΔS) for a process can be expressed as:
ΔS=Cpln(T2T1)−Rln(P2P1)
- Here, Cp is the heat capacity at constant pressure, T1 and T2 are the initial and final temperatures, and R is the universal gas constant.
- Since the process is isobaric, we have P1=P2. Therefore, the term ln(P2P1) becomes ln(1), which is equal to 0.
- With the above simplification, the equation for ΔS reduces to:
ΔS=Cpln(T2T1)
- Thus, the change in entropy during the isobaric process when the temperature changes from T1 to T2 is given by:
ΔS=Cpln(T2T1)
Similar Questions
n moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View SolutionA certain amount of water of mass m, at a temperature T2 cools.to temperature T1. The heat given out by the water is absorbed by n mole of an ideal gas. The gas expands at constant temperature T and changes its volume from Vi to Vf What is its initial volume ?
View Solution
Knowledge Check
Pressure P, volume V and temperature T for a certain gas are related by P=AT−BT2V, where A and B are constatns .The work done by the gas as its temperature change from T1 to T2 while pressure remaining constatn is
AA−B2(R2−T1)BA(T2−T1)−B(T22−T21)CA2(T22−T21)−B3(T32−T31)DA(T2−T1)−B3(T2−T1)3A monatomic gas on n molecules is heated from temperature T1 to T2 under two different conditions (i) constant volume, (ii) constant pressure. The change of internal energy of the gas
Amore of (i)Bmore of (ii)Csame in both casesDindependent of number of moles
The amount of heat energy required to raise the temperature of 1 g of Helium at NTP, from T1 K to T2 K is :
View Solution
As shown in figure process AB is isobaric, BC is adiabasic CD is isochoric and DA is isothermal, through which n-moles of monoatomic gas undergo a cyclic process. The max & min temperature in the cycle are 4T0 and T0 respectively.
View SolutionFor a reaction A→P, the plots of [A] and [P] with time at temperatures T1 and T2 are given below.
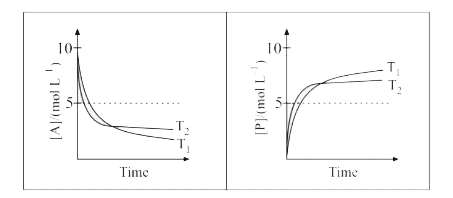
If T1>T2, the correct statements is (are):
(Assume ΔHΘ and ΔSΘ are independent of temperature and ratio of ln K at T1 to ln K at T2 is greater than T2T1. Here H,S,G and K are enthalpy, entropy, Gibbs energy and equilibrium constant, respectively).
View SolutionTwo samples 1 and 2 are initially kept in the same state. The sample 1 is expanded through an isothermal process where as sample 2 through an adiabatic process upto the same final volume. The final temperature in process 1 and 2 are T1 and T2 respectively, then
View SolutionTwo samples 1 and 2 are initially kept in the same state. The sample 1 is expanded through an isothermal process where as sample 2 through an adiabatic process upto the same final volume. The final temperature in process 1 and 2 are T1 and T2 respectively, then
View SolutionAn ideal monatomic gas undergoes a process where its pressure is inversely proportional to its temperature.
(a) Calculate the molar specific heat of the process.
(b) Find the work done by two moles of gas if the temperature change from T1 to T2.
View Solution
