In an isobaric process of an ideal gas. The ratio of heat supplied annd work done by the system [i.e.,(QW)] is
γ−1γ
γ
γγ−1
1
The correct Answer is:C
To solve the problem, we need to find the ratio of heat supplied (Q) to the work done (W) in an isobaric process for an ideal gas. Let's break it down step by step.
Step 1: Understand the Isobaric Process
In an isobaric process, the pressure (P) remains constant.
Step 2: Write the Expression for Heat Supplied (Q)
For an ideal gas undergoing an isobaric process, the heat supplied (Q) can be expressed as:
Q=nCpΔT
where:
- n = number of moles of the gas
- Cp = molar specific heat capacity at constant pressure
- ΔT = change in temperature
Step 3: Write the Expression for Work Done (W)
The work done (W) by the gas during an isobaric process is given by:
W=PΔV
Using the ideal gas law, we can express this as:
W=nRΔT
where:
- R = universal gas constant
Step 4: Find the Ratio QW
Now, we can find the ratio of heat supplied to work done:
QW=nCpΔTnRΔT
Here, n and ΔT cancel out:
QW=CpR
Step 5: Relate Cp and Cv Using γ
We know that:
Cp−Cv=R
and the ratio of specific heats is defined as:
γ=CpCv
From this, we can express Cp in terms of γ and Cv:
Cp=γCv
Substituting Cv=Cp−R into the equation gives:
Cp=γ(Cp−R)
Rearranging this, we find:
Cp(1−γ)=−γR
Thus:
Cp=Rγγ−1
Step 6: Substitute Cp Back into the Ratio
Now substituting Cp back into our ratio:
QW=CpR=Rγγ−1R
The R cancels out:
QW=γγ−1
Conclusion
Thus, the ratio of heat supplied to work done in an isobaric process is:
QW=γγ−1
Final Answer
The correct option is γγ−1.
In an isobaric process, the pressure (P) remains constant.
For an ideal gas undergoing an isobaric process, the heat supplied (Q) can be expressed as:
Q=nCpΔT
where:
- n = number of moles of the gas
- Cp = molar specific heat capacity at constant pressure
- ΔT = change in temperature
The work done (W) by the gas during an isobaric process is given by:
W=PΔV
Using the ideal gas law, we can express this as:
W=nRΔT
where:
- R = universal gas constant
Now, we can find the ratio of heat supplied to work done:
QW=nCpΔTnRΔT
Here, n and ΔT cancel out:
QW=CpR
We know that:
Cp−Cv=R
and the ratio of specific heats is defined as:
γ=CpCv
From this, we can express Cp in terms of γ and Cv:
Cp=γCv
Substituting Cv=Cp−R into the equation gives:
Cp=γ(Cp−R)
Rearranging this, we find:
Cp(1−γ)=−γR
Thus:
Cp=Rγγ−1
Now substituting Cp back into our ratio:
QW=CpR=Rγγ−1R
The R cancels out:
QW=γγ−1
Thus, the ratio of heat supplied to work done in an isobaric process is:
QW=γγ−1
The correct option is γγ−1.
Similar Questions
In an isobaric process, the ratio of heat supplied to the system (dQ) and work done by the system (dW) for diatomic gas is
View Solutionif work is done by the system then W is
View SolutionThe internal enegy of an ideal gas decreases by the same amount as the work done by the system.
View SolutionAssertion : For an isothermal process in an ideal gas, the heat obsorbed by the gas is entirely used in the work done by the gas.
Reason : During a process taking place in a system, the temperature remains constant then the process is isothermal.
View SolutionIn an isobaric process, heat is supplied to a monoatomic ideal gas. The fraction of heat that goes itno mechanical work is
View SolutionAn ideal monoatomic gas undergoes the process AB as shown in the figure. If the heat supplied and the work done in the process are ΔQ and Delta Wrespectively.TheratioDeltaQ : DeltaW is
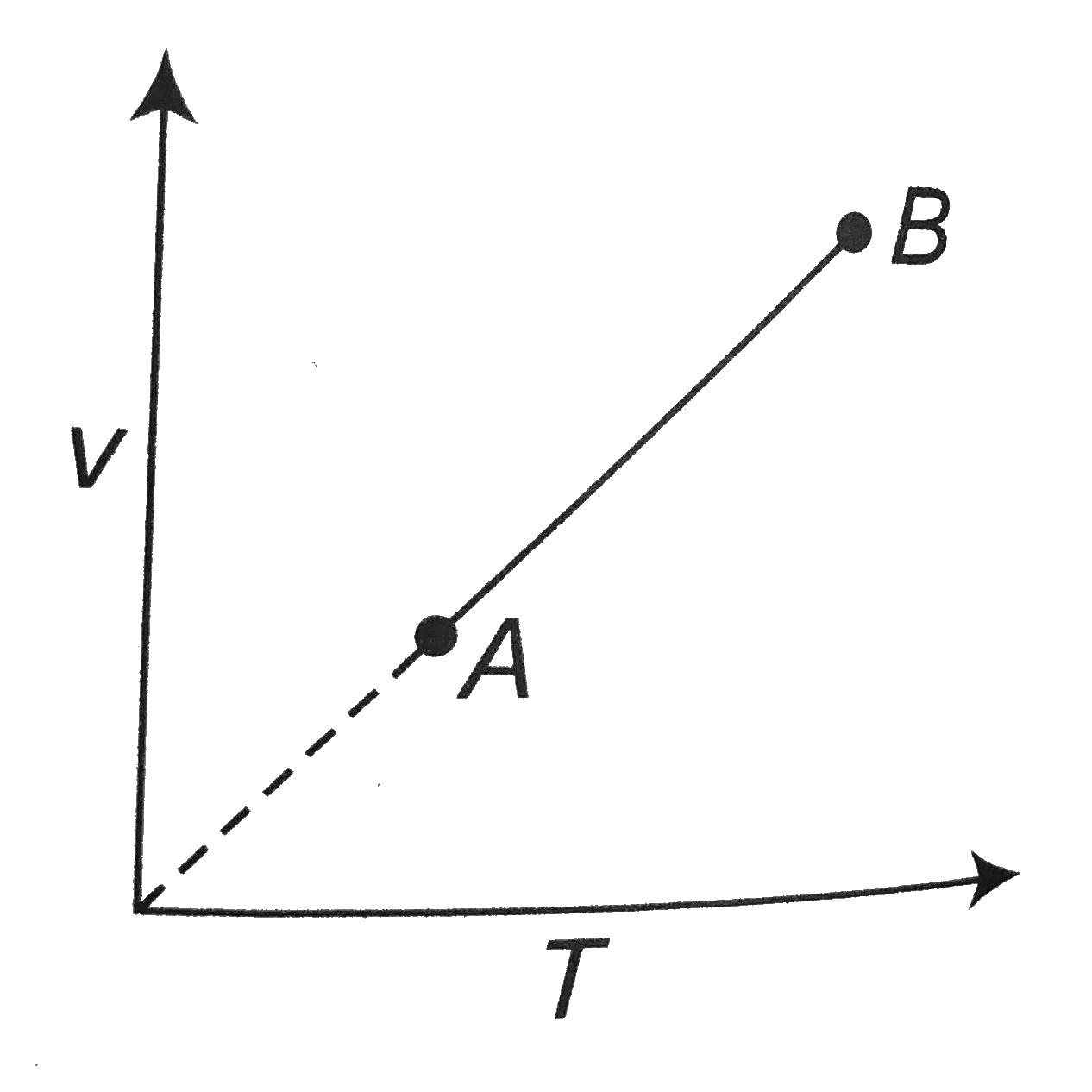
View Solutionn moles of an ideal gas with constant volume heat capacity CV undergo an isobaric expansion by certain volumes. The ratio of the work done in the process, to the heat supplied is:
View SolutionIf heat is supplied to an ideal gas in an isothermal process.
View SolutionAn ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. The ratio of heat absorbed during AB to the work done on the gas during BC id
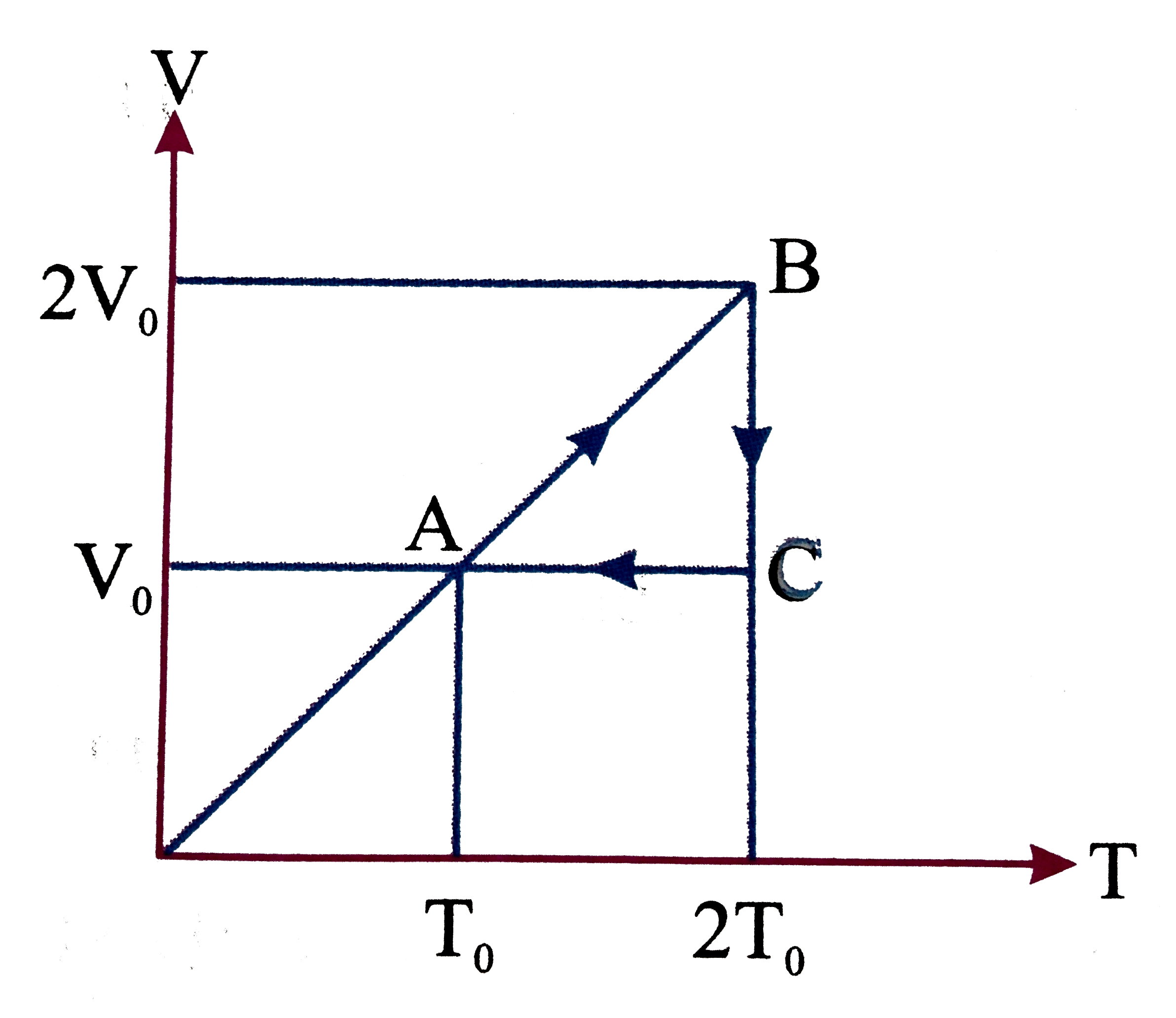
View Solution550kJcycle−1 work is done by 1 mol of an ideal gas in a cyclic process. The amount of heat absorbed by the system in one cycle is
View Solution
