A wire of mass 100 g, length 1 m and current 5 A is balanced in mid air by a magnetic field B, then find the value of B.
a. 0.2 T
b. 0.1 T
c. 0.5 T
d. 0.6 T
The correct Answer is:A
To solve the problem, we need to find the value of the magnetic field B that balances the weight of a wire carrying a current. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the wire, m=100g=0.1kg (since 1g=10−3kg)
- Length of the wire, l=1m
- Current through the wire, I=5A
- Acceleration due to gravity, g=9.8m/s2
Step 2: Calculate the weight of the wire
The weight W of the wire can be calculated using the formula:
W=m⋅g
Substituting the values:
W=0.1kg⋅9.8m/s2=0.98N
Step 3: Use the formula for the magnetic force
The magnetic force FB acting on the wire can be calculated using the formula:
FB=I⋅l⋅B
Where:
- I is the current in the wire,
- l is the length of the wire,
- B is the magnetic field strength.
Step 4: Set the magnetic force equal to the weight
Since the wire is balanced in mid-air, the magnetic force must equal the weight of the wire:
FB=W
Thus,
I⋅l⋅B=m⋅g
Step 5: Solve for the magnetic field B
Rearranging the equation to solve for B:
B=m⋅gI⋅l
Substituting the known values:
B=0.1kg⋅9.8m/s25A⋅1m=0.98N5A=0.196T
Step 6: Round the answer
Rounding 0.196T to two decimal places gives:
B≈0.2T
Final Answer
The value of the magnetic field B is approximately 0.2 T.
---
- Mass of the wire, m=100g=0.1kg (since 1g=10−3kg)
- Length of the wire, l=1m
- Current through the wire, I=5A
- Acceleration due to gravity, g=9.8m/s2
The weight W of the wire can be calculated using the formula:
W=m⋅g
Substituting the values:
W=0.1kg⋅9.8m/s2=0.98N
The magnetic force FB acting on the wire can be calculated using the formula:
FB=I⋅l⋅B
Where:
- I is the current in the wire,
- l is the length of the wire,
- B is the magnetic field strength.
Since the wire is balanced in mid-air, the magnetic force must equal the weight of the wire:
FB=W
Thus,
I⋅l⋅B=m⋅g
Rearranging the equation to solve for B:
B=m⋅gI⋅l
Substituting the known values:
B=0.1kg⋅9.8m/s25A⋅1m=0.98N5A=0.196T
Rounding 0.196T to two decimal places gives:
B≈0.2T
The value of the magnetic field B is approximately 0.2 T.
Similar Questions
A straight wire of mass 400 g and length 2m carries a current of 2A. It is suspended in mid air by a uniform horizontal field B. What is the magnitude of the magnetic field ?
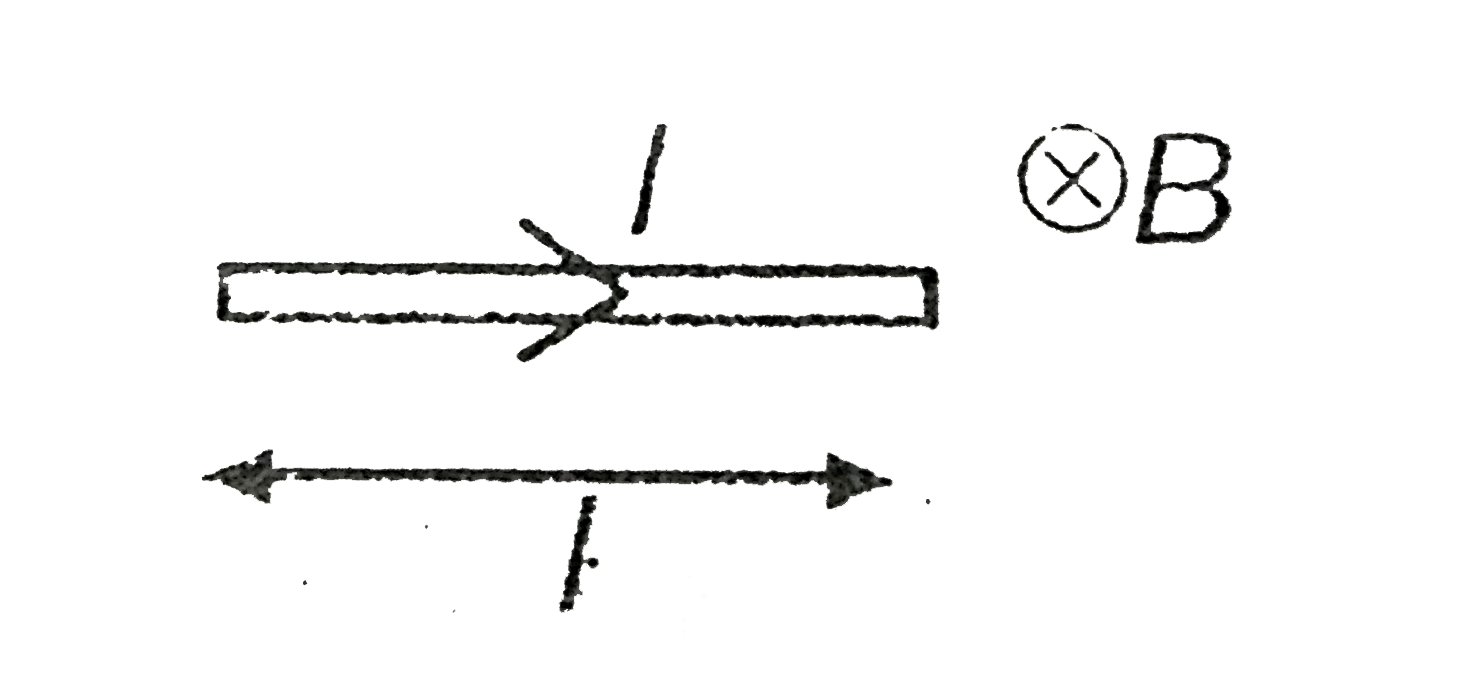
View SolutionA straight wire of mass 400 g and length 2m carries a current of 2A. It is suspended in mid air by a uniform horizontal field B. What is the magnitude of the magnetic field ?

View Solution
Knowledge Check
A straight wire having mass of 1.2 kg and length of 1m carries a current of 5 A. If the wire is suspended in mid-air by a uniform horizontal magnetic field, then the magnitude of field is
A0.65TB1.53TC2.4TD3.2T
A wire of length 100 m is tightly wounded on a hollow tube of radius 5mm and length 1 m. A current of 1 A is flowing in the wire. Then magnetic field strength inside the tube will be :-
View SolutionA straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid-air by a uniform horizontal magnetic field B. What is the magnitude of the magnetic field?

View SolutionA straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid-air by a uniform horizontal magnetic field B. What is the magnitude of the magnetic field?

View SolutionA straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid-air by a uniform horizontal magnetic field B. What is the magnitude of the magnetic field?

View SolutionA conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
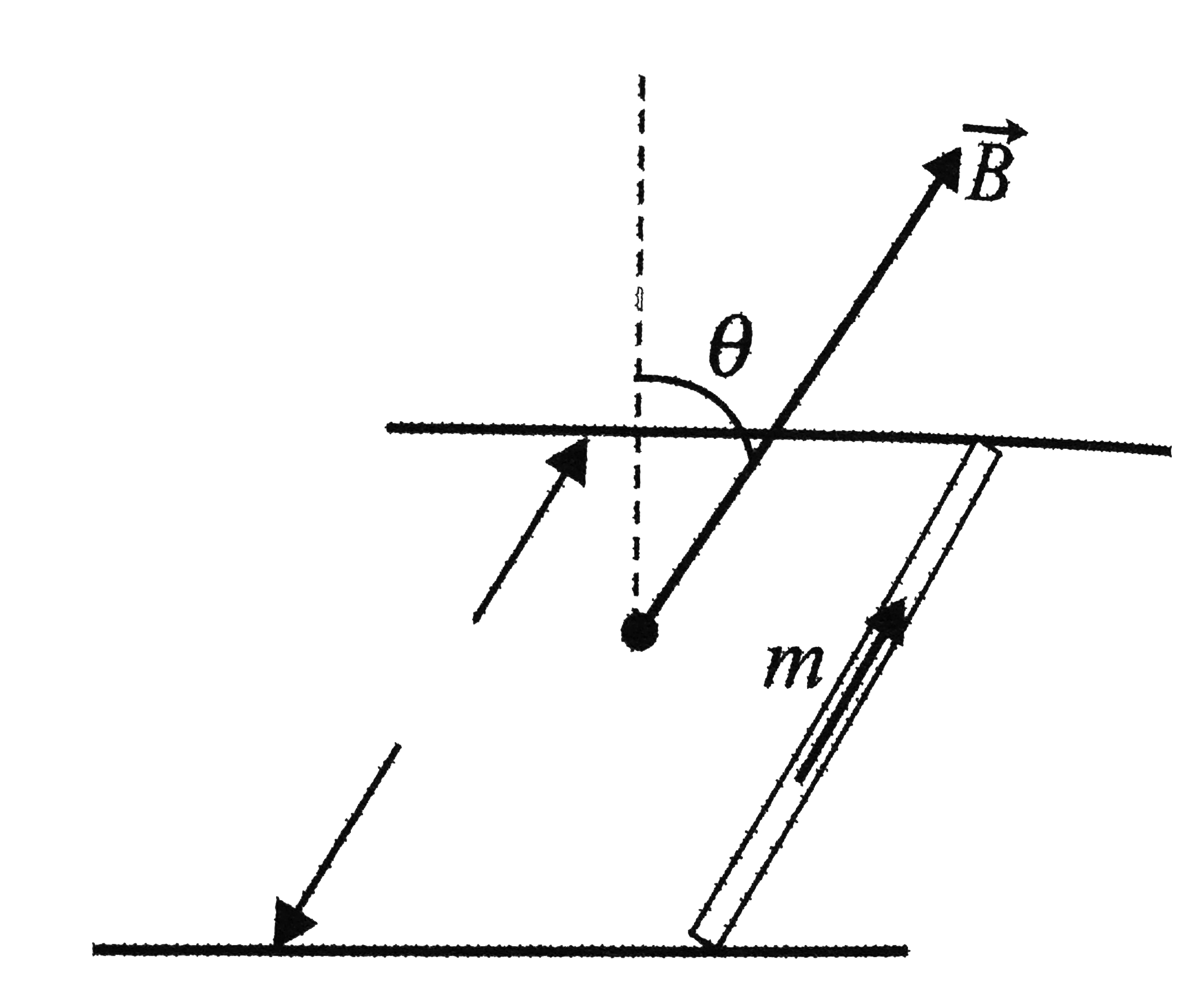
View SolutionA straight horizontal wire of mass 10mg and length 1.0 cm carries a current of 2.0 A. what minimum megnetic field B should be applied in the region so that the magnetic force on the wire may balance its weight?
View SolutionA straight wire of length 0.5 metre and carrying a current of 1.2 ampere is placed in a uniform magnetic field of induction 2 tesla. If the magnetic field is perpendicular to the length of the wire , the force acting on the wire is
View Solution
