The minimum magnetic dipole moment of electron in hydrogen atom is
eh2πm
eh4πm
ehπm
0
The correct Answer is:B
To find the minimum magnetic dipole moment of an electron in a hydrogen atom, we can follow these steps:
1. Understanding Magnetic Dipole Moment:
The magnetic dipole moment (μ) for a current-carrying loop is given by the formula:
μ=I×A
where I is the current and A is the area of the loop.
2. Area of the Circular Path:
For an electron revolving in a circular path of radius r, the area A is:
A=πr2
3. Calculating the Current:
The current I due to the electron can be expressed as the charge e divided by the time T it takes to complete one revolution:
I=eT
The time period T can be related to the angular speed ω by:
T=2πω
4. Angular Momentum:
According to Bohr's model, the angular momentum L of the electron is quantized:
L=nh2π
where n is the principal quantum number and h is Planck's constant.
5. Relating Angular Momentum to Current:
The angular momentum can also be expressed as:
L=I⋅ω⋅r2
Substituting I from Step 3:
L=(eT)⋅ω⋅r2
6. Substituting for Time Period:
We can substitute T from Step 3 into the angular momentum equation:
L=(e⋅ω2π)⋅2πω⋅r2=e⋅r2⋅ω2π
7. Finding the Expression for Magnetic Moment:
Now substituting L into the magnetic dipole moment equation:
μ=I⋅A=eT⋅πr2=e⋅ω2π⋅πr2=e⋅r2⋅ω2
8. Using the Angular Momentum Expression:
From the angular momentum expression, we can express r in terms of n:
r=nh2πmω
Substitute this back into the magnetic moment equation to find the minimum value when n=1.
9. Final Expression for Minimum Magnetic Moment:
After simplification, we find:
μ=nhe4πm
For the minimum case n=1:
μmin=he4πm
Conclusion:
The minimum magnetic dipole moment of the electron in a hydrogen atom is:
μmin=eh4πm
The magnetic dipole moment (μ) for a current-carrying loop is given by the formula:
μ=I×A
where I is the current and A is the area of the loop.
For an electron revolving in a circular path of radius r, the area A is:
A=πr2
The current I due to the electron can be expressed as the charge e divided by the time T it takes to complete one revolution:
I=eT
The time period T can be related to the angular speed ω by:
T=2πω
According to Bohr's model, the angular momentum L of the electron is quantized:
L=nh2π
where n is the principal quantum number and h is Planck's constant.
The angular momentum can also be expressed as:
L=I⋅ω⋅r2
Substituting I from Step 3:
L=(eT)⋅ω⋅r2
We can substitute T from Step 3 into the angular momentum equation:
L=(e⋅ω2π)⋅2πω⋅r2=e⋅r2⋅ω2π
Now substituting L into the magnetic dipole moment equation:
μ=I⋅A=eT⋅πr2=e⋅ω2π⋅πr2=e⋅r2⋅ω2
From the angular momentum expression, we can express r in terms of n:
r=nh2πmω
Substitute this back into the magnetic moment equation to find the minimum value when n=1.
After simplification, we find:
μ=nhe4πm
For the minimum case n=1:
μmin=he4πm
The minimum magnetic dipole moment of the electron in a hydrogen atom is:
μmin=eh4πm
Similar Questions
Knowledge Check
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
Aeh4πmBeh2πmCeh24πmDe2h4πm
With reference to magnetic dipole, match the tems of Column I with the tems of Column Ii and Choose the correct option from the codes given below.

View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
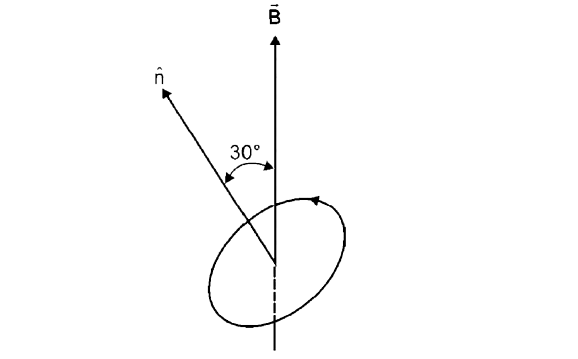
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
View SolutionThe ratio of magnetic dipole moment of an electron of charge e and mass m in the Bohr orbit in hydrogen to the angular momentum of the electron in the orbit is:
View SolutionCalculate the change in magnetic dipole moment when the electron in a H−atom makes a transition from the n=4 orbit to the n=3 orbit. Suppose that the atoms is in a magnetic field of induction. Calculate the change in energy when it makes the same transition and the corresponding change in frequency of the emitted photon due to the magnetic field.
View SolutionDeduce an expression for the magnetic dipole moment of an electron orbiting around the central nucleus.
View SolutionMagnetic dipole moment of rectangular loop is
View SolutionThe minimum orbital angular momentum of the electron in a hydrogen atom is
View Solution
