Two wires carrying
Parallel current repel each other.
Antiparallel current attract each other.
Antiparallel current repel each other.
Equal magnitudes of antiparallel current attract each other.
The correct Answer is:C
To solve the problem regarding the forces between two wires carrying currents, we can break down the solution into clear steps.
1. Understanding the Setup:
- We have two long parallel wires. Let’s denote them as Wire 1 and Wire 2.
- Wire 1 carries a current I1 and Wire 2 carries a current I2.
2. Direction of Currents:
- For the first case, assume both wires carry currents in the same direction (parallel currents).
- For the second case, assume the currents are in opposite directions (antiparallel currents).
3. Magnetic Field Due to a Current-Carrying Wire:
- The magnetic field B created by a long straight wire at a distance r from it is given by:
B=μ0I2πr
- Here, μ0 is the permeability of free space.
4. Force on a Current-Carrying Wire:
- The force F on a segment of wire of length L carrying current I in a magnetic field B is given by:
F=IL×B
- The direction of the force can be determined using the right-hand rule.
5. Calculating the Force for Parallel Currents:
- For Wire 1, the magnetic field at the location of Wire 2 (due to Wire 1) is:
B1=μ0I12πr
- The force on Wire 2 due to Wire 1 is:
F12=I2LB1=I2L(μ0I12πr)
- The direction of this force is attractive (both wires pull towards each other).
6. Calculating the Force for Antiparallel Currents:
- For antiparallel currents, the magnetic field direction remains the same, but the force direction changes.
- The force on Wire 2 due to Wire 1 is still given by:
F12=I2LB1=I2L(μ0I12πr)
- However, this time the force is repulsive (the wires push away from each other).
7. Conclusion:
- For parallel currents, the force is attractive.
- For antiparallel currents, the force is repulsive.
Final Answer:
- Parallel currents attract each other, while antiparallel currents repel each other.
- We have two long parallel wires. Let’s denote them as Wire 1 and Wire 2.
- Wire 1 carries a current I1 and Wire 2 carries a current I2.
- For the first case, assume both wires carry currents in the same direction (parallel currents).
- For the second case, assume the currents are in opposite directions (antiparallel currents).
- The magnetic field B created by a long straight wire at a distance r from it is given by:
B=μ0I2πr
- Here, μ0 is the permeability of free space.
- The force F on a segment of wire of length L carrying current I in a magnetic field B is given by:
F=IL×B
- The direction of the force can be determined using the right-hand rule.
- For Wire 1, the magnetic field at the location of Wire 2 (due to Wire 1) is:
B1=μ0I12πr
- The force on Wire 2 due to Wire 1 is:
F12=I2LB1=I2L(μ0I12πr)
- The direction of this force is attractive (both wires pull towards each other).
- For antiparallel currents, the magnetic field direction remains the same, but the force direction changes.
- The force on Wire 2 due to Wire 1 is still given by:
F12=I2LB1=I2L(μ0I12πr)
- However, this time the force is repulsive (the wires push away from each other).
- For parallel currents, the force is attractive.
- For antiparallel currents, the force is repulsive.
- Parallel currents attract each other, while antiparallel currents repel each other.
Similar Questions
Two long wires carrying current are kept crossed ( not joined at ) . The locus where magnetic field is zero is -
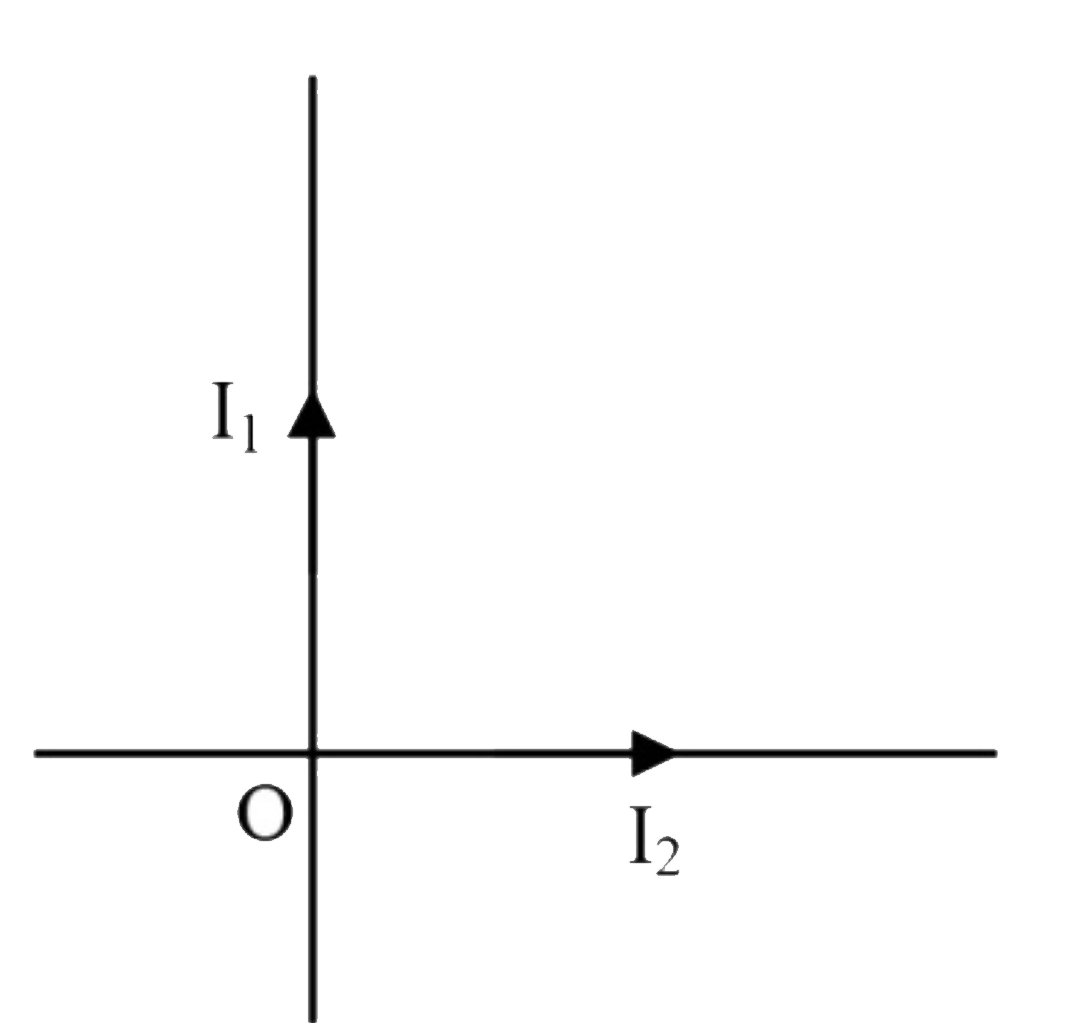
View SolutionTwo long wires carrying same currents in opposite directions are placed at separation D as shown.Predict variation of magnetic field as one moves from the point O and A
View SolutionFigure. Shows two long wires carrying equal currents I1andI2 flowing in opposite directions. Which of the arrows labeled A to D correctely represents the direction of the magnetic field due to the wires at a point located at an equal distance d from each wire?
View SolutionTwo very long wires carrying equal current i are bent and arranged as shown in figure. Both AB and CD are arcs of the same circle, both subtending right angles at the centre O. The magnetic field at O is:

View Solution
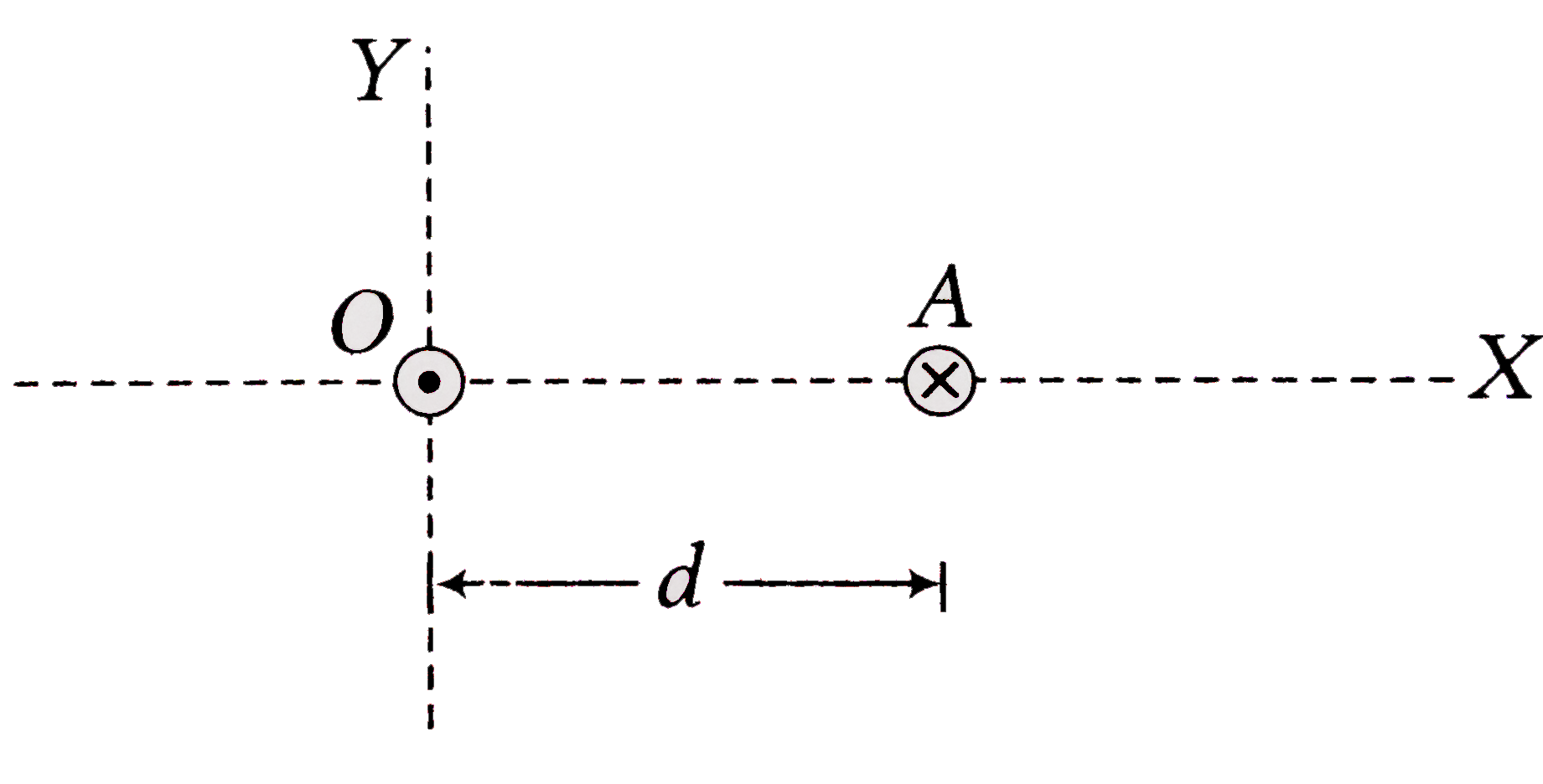
Two long wires carrying current I1andI2 are arranged as shown in figure the one carrying current I1 is along is the x-axis. The other carrying current I2 is along a line parallel to the y-axis given by x=0 and z=d. Find the force exerted at O2 because of the wire along the x-axis.
View SolutionThree infinite current carrying conductors are placed as shown in Fig. Two wires carry same current while current in third wire is unknown. The three wires are electrically insulated from each other and all of them are in the plane of paper. Which of the following is correct about point P which is also in the same plane?
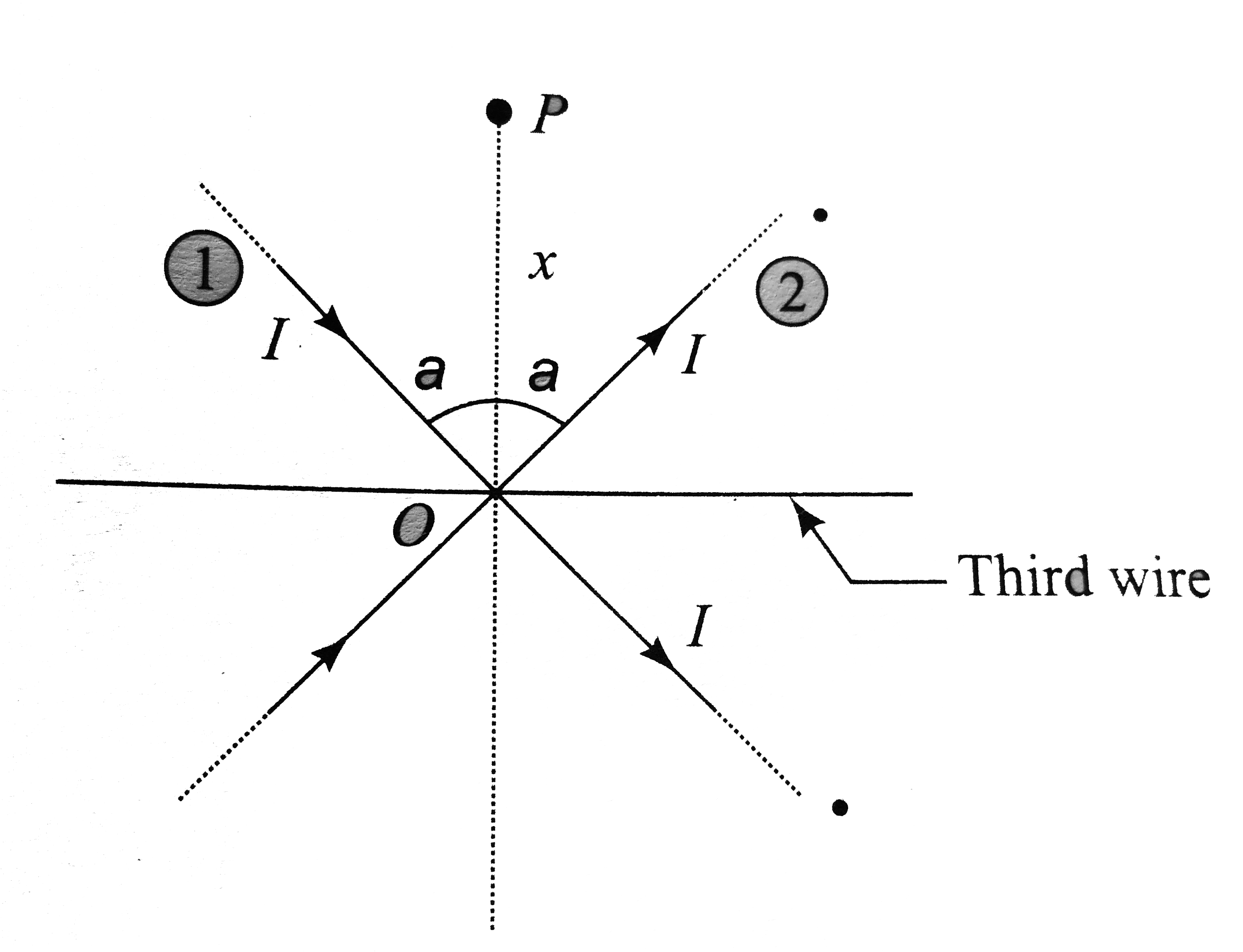
View SolutionThree infinite current carrying conductors are placed as shown in Fig. Two wires carry same current while current in third wire is unknown. The three wires are electrically insulated from each other and all of them are in the plane of paper. Which of the following is correct about point P which is also in the same plane?

View Solutiontwo infinite wires, carrying currents i1andi2., are lying along x-and y-axes, as shown in the x-y plane. Then,
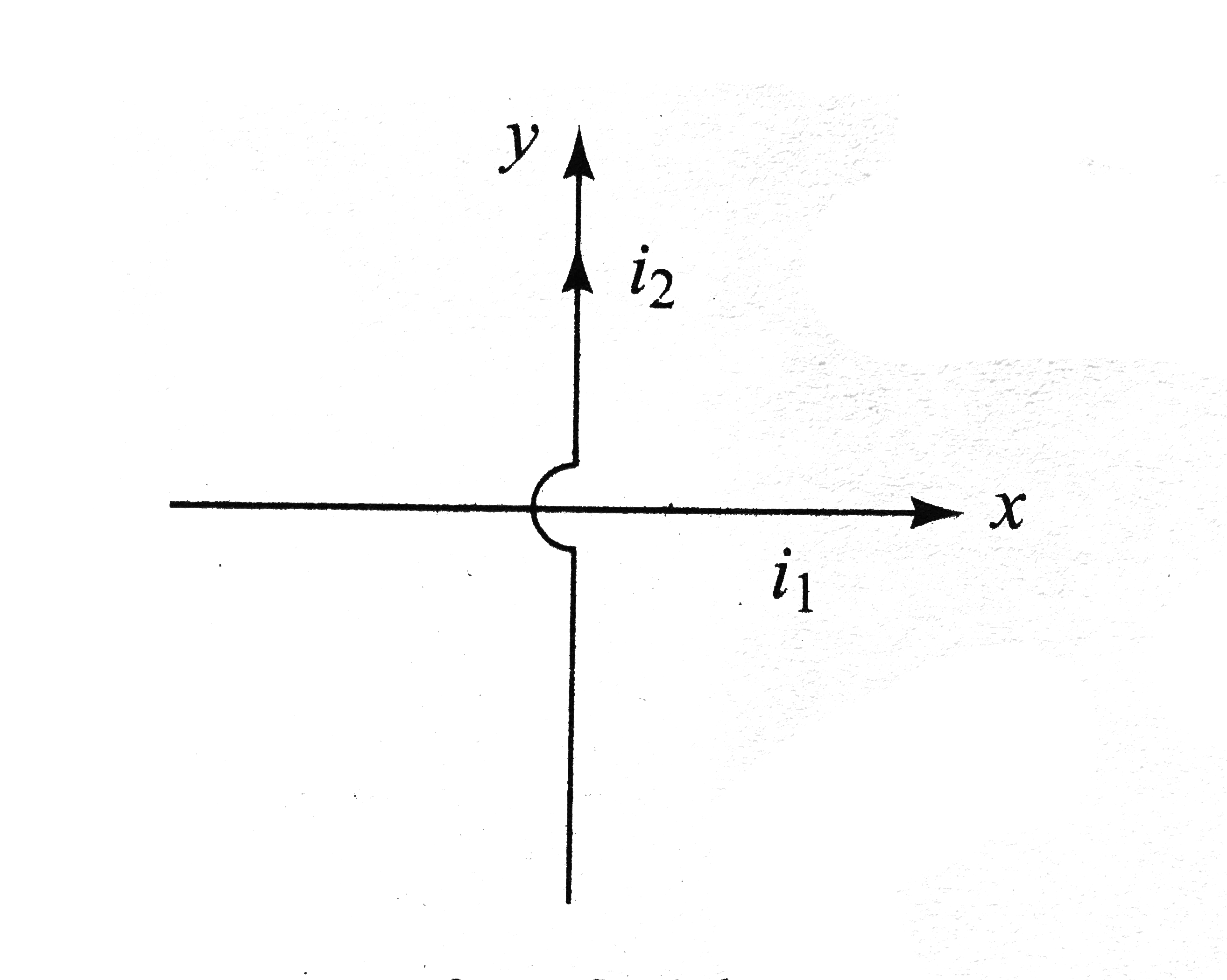
View SolutionWhen two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
View SolutionThe two long, straight wires carrying electric currents in opposite directions. The separation between the wires is 5.0 cm. Find the magnetic field at a point P midway between the wires.
View Solution
