In bcc structure contribution of corner and central atom is
18,1
14,18
18,12
1,12
To solve the question regarding the contribution of corner and central atoms in a body-centered cubic (BCC) structure, we can follow these steps:
1. Understanding the BCC Structure:
- A body-centered cubic (BCC) structure consists of atoms located at the corners of a cube and one atom at the center of the cube.
2. Counting the Corner Atoms:
- In a BCC structure, there are 8 corners. Each corner atom is shared among 8 adjacent unit cells.
3. Calculating Contribution from Corner Atoms:
- Since each corner atom is shared by 8 unit cells, the contribution of each corner atom to a single unit cell is 18.
- Therefore, the total contribution from all 8 corner atoms is:
8×18=1
4. Identifying the Central Atom:
- The BCC structure has one atom located at the center of the cube. This central atom is not shared with any other unit cell.
5. Calculating Contribution from the Central Atom:
- Since the central atom is entirely within the unit cell, its contribution is 1.
6. Summarizing Contributions:
- The total contributions are:
- Contribution from corner atoms: 1
- Contribution from the central atom: 1
- Therefore, the contributions can be summarized as:
- Corner contribution: 18 per corner atom, total from 8 corners = 1
- Central atom contribution: 1
7. Final Answer:
- The contributions of the corner and central atoms in a BCC structure are 18 for each corner atom (totaling 1 from all corners) and 1 for the central atom.
Conclusion:
- The correct answer is: Contribution of corner atoms = 18 and contribution of the central atom = 1.
- A body-centered cubic (BCC) structure consists of atoms located at the corners of a cube and one atom at the center of the cube.
- In a BCC structure, there are 8 corners. Each corner atom is shared among 8 adjacent unit cells.
- Since each corner atom is shared by 8 unit cells, the contribution of each corner atom to a single unit cell is 18.
- Therefore, the total contribution from all 8 corner atoms is:
8×18=1
- The BCC structure has one atom located at the center of the cube. This central atom is not shared with any other unit cell.
- Since the central atom is entirely within the unit cell, its contribution is 1.
- The total contributions are:
- Contribution from corner atoms: 1
- Contribution from the central atom: 1
- Therefore, the contributions can be summarized as:
- Corner contribution: 18 per corner atom, total from 8 corners = 1
- Central atom contribution: 1
- The contributions of the corner and central atoms in a BCC structure are 18 for each corner atom (totaling 1 from all corners) and 1 for the central atom.
- The correct answer is: Contribution of corner atoms = 18 and contribution of the central atom = 1.
Similar Questions
Knowledge Check
CF4,SF4andXeF4 contain the following electronic structure on their central atoms. Which one is correct option ?
A1, 2 and 3 lone pairs of electrons respectivelyB0,1 and 2 lone pairs of electrons respectivelyC1,1 and 1 lone pairs of electrons respectivelyDNo lone pairs of electrons on anly moleculeLess contributing structure of nitroethene is :
A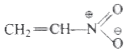 B
B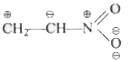 C
C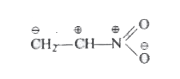 D
D
Most contributing structure in nitroethene is :
A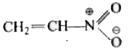 B
B C
C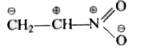 D
D
In bcc structure of lattice constant a, the minimum distance between atoms is
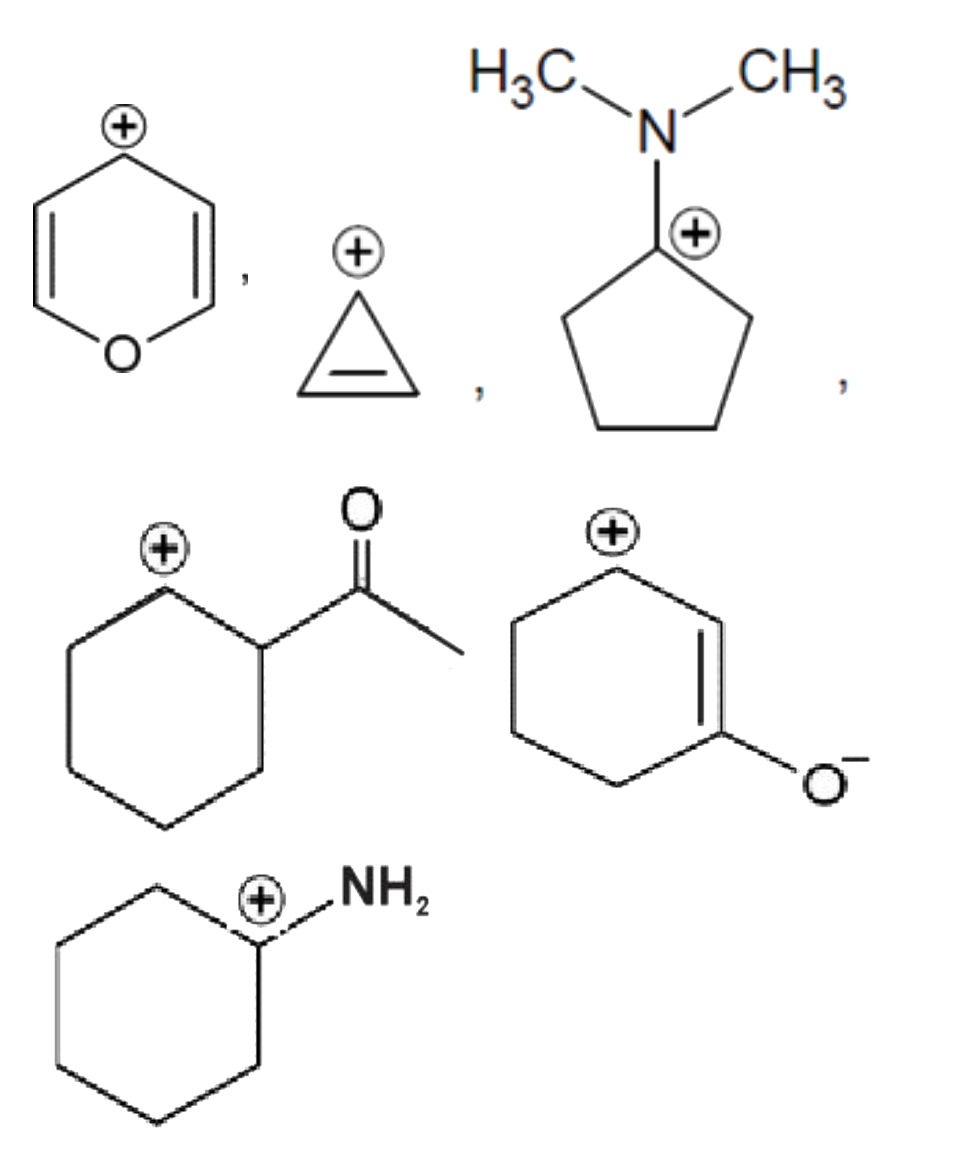
View SolutionHow many of the following intermediates heve at least one contributing structure in which all atoms have their octet complete ?
View SolutionDraw the structure of xenon tetrafluoride molecule. State the hybridisation of the central atom and the geometry of the molecule.
View SolutionFor the molecule of IF7 :
(i) Draw the structure of the molecule
(ii) State the hybridization of the central atom.
(iii) State the geomtry of the molecule.
View SolutionWhich of the following structures contribute most to the tensile strength of loose connective tissues?
View Solution
