A cart of mass 150 kg is pulled horizontally on a frictionless surface with face 10 N. If 100 g/s sand is being dropped in the cart verticlly then find the speed of the system when cart has 100 kg snad in it.
10 m/s
20 m/s
40 m/s
50 m/s
The correct Answer is:C
To solve the problem step-by-step, we will use the principles of momentum and the concept of thrust force due to the sand being dropped into the cart.
Step 1: Identify the given values
- Mass of the cart, m0=150kg
- Force applied, F=10N
- Rate of sand being dropped, μ=100g/s=0.1kg/s
- Mass of sand when the cart has 100 kg of sand, m=100kg
Step 2: Determine the total mass of the system
The total mass of the system when the cart has 100 kg of sand is:
M=m0+m=150kg+100kg=250kg
Step 3: Set up the equation of motion
The thrust force due to the sand being dropped is given by:
Thrust force=μv
The net force acting on the system can be expressed as:
F−μv=Mdvdt
Where dv/dt is the acceleration of the system.
Step 4: Rearranging the equation
Rearranging gives:
F−μv=d(Mv)dt
Since the mass is changing due to the sand being added, we can express this as:
F−μv=ddt(Mv)=Mdvdt+vdmdt
Here, dmdt=μ.
Step 5: Substitute values
Substituting the values we have:
10−0.1v=250dvdt+v(0.1)
This simplifies to:
10−0.1v=250dvdt+0.1v
Combining terms gives:
10=250dvdt+0.2v
Step 6: Solve for velocity
Now we need to integrate this equation. We can express it as:
dvdt=10−0.2v250
Integrating both sides will give us the velocity as a function of time.
Step 7: Find the final velocity when the mass is 250 kg
Assuming that the system starts from rest, we can integrate to find the final speed when the cart has 100 kg of sand.
Using the relationship:
v=FtM+μt
Substituting F=10N, M=150kg+100kg=250kg, and μ=0.1kg/s:
v=10t150+0.1t
To find the time when the cart has 100 kg of sand:
100=0.1t⟹t=1000s
Now substituting t=1000s into the velocity equation:
v=10×1000150+0.1×1000=10000150+100=10000250=40m/s
Final Answer
Thus, the speed of the system when the cart has 100 kg of sand in it is:
40m/s
- Mass of the cart, m0=150kg
- Force applied, F=10N
- Rate of sand being dropped, μ=100g/s=0.1kg/s
- Mass of sand when the cart has 100 kg of sand, m=100kg
The total mass of the system when the cart has 100 kg of sand is:
M=m0+m=150kg+100kg=250kg
The thrust force due to the sand being dropped is given by:
Thrust force=μv
The net force acting on the system can be expressed as:
F−μv=Mdvdt
Where dv/dt is the acceleration of the system.
Rearranging gives:
F−μv=d(Mv)dt
Since the mass is changing due to the sand being added, we can express this as:
F−μv=ddt(Mv)=Mdvdt+vdmdt
Here, dmdt=μ.
Substituting the values we have:
10−0.1v=250dvdt+v(0.1)
This simplifies to:
10−0.1v=250dvdt+0.1v
Combining terms gives:
10=250dvdt+0.2v
Now we need to integrate this equation. We can express it as:
dvdt=10−0.2v250
Integrating both sides will give us the velocity as a function of time.
Assuming that the system starts from rest, we can integrate to find the final speed when the cart has 100 kg of sand.
v=FtM+μt
Substituting F=10N, M=150kg+100kg=250kg, and μ=0.1kg/s:
v=10t150+0.1t
100=0.1t⟹t=1000s
v=10×1000150+0.1×1000=10000150+100=10000250=40m/s
Thus, the speed of the system when the cart has 100 kg of sand in it is:
40m/s
Similar Questions
A cart is moving with a velocity 20m/s. Sand is being dropped into the cart at the rate of 50 kg/min. The force required to move the cart with constant velocity will be :-
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

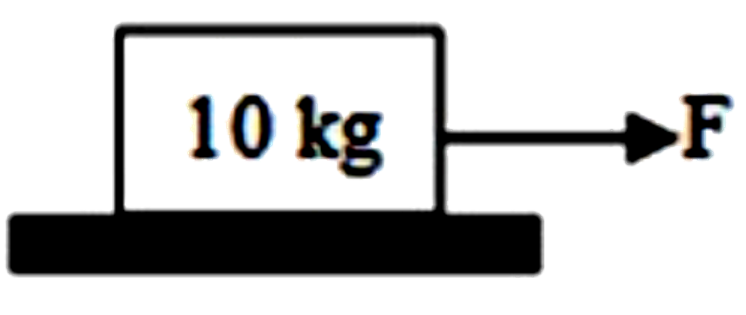
View SolutionA force F=2t2 is applied to the cart of mass 10 Kg, initially at rest. The speed of the cart at t = 5 s is -
View SolutionA toy cart of mass √3 kg is pulled by a force of 20N at an angle of 30∘ with the frictionless horizontal surface on which the cart is placed. The cart shall move on the surface with an acceleration .
View SolutionA cart is moving horizontally along a straight line with constant speed 30 m/s. A projectile is to be fired from the moving cart in such a way that it will return to the cart after the cart has moved 120m. At what speed (relative to the cart, in m/s) must the projectile be fired ? (Take g=10m/s2)
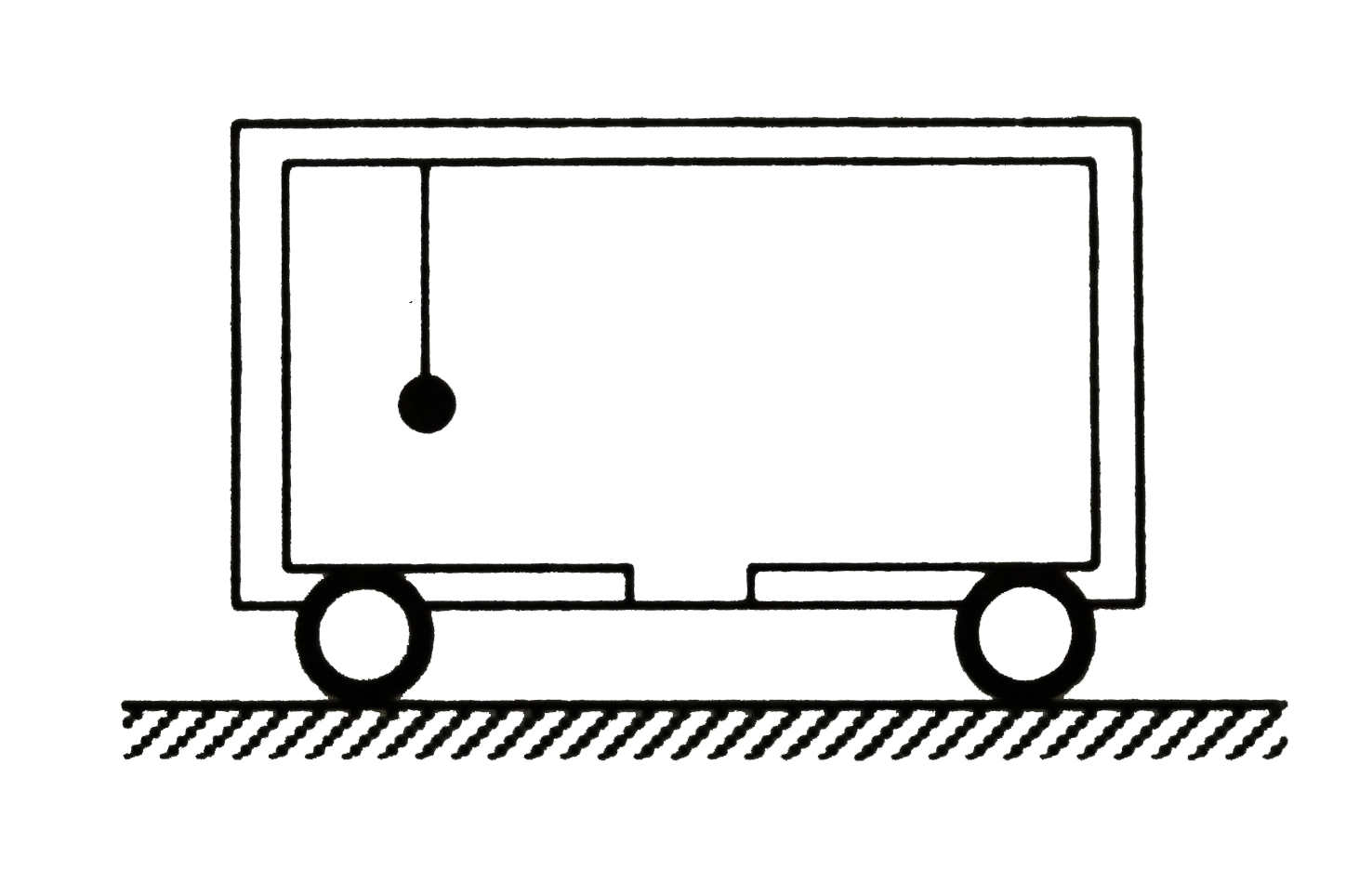
View SolutionA cart of mas M is at rest on a frictionless horizontal surface and a pendulum bob of mass m hangs from the roof of the cart figure. The string breaks, the bob falls on the floor, makes several collision on the floor and finally lands up in a small slot made in the floor. The horizontal distance between the string and the slot is L. Find the displacement of the cart during this process
View SolutionA cannon of mass 100 kg is kept on a frictionless floor. If a cannon ball of mass 1 kg is fired from it with a speed of 200 m/s. With what velocity the cannon will move ?
View Solution
