Considering normal incidence of ray, the equivalent refractive index of combination of two slabs shown in Fig. is.
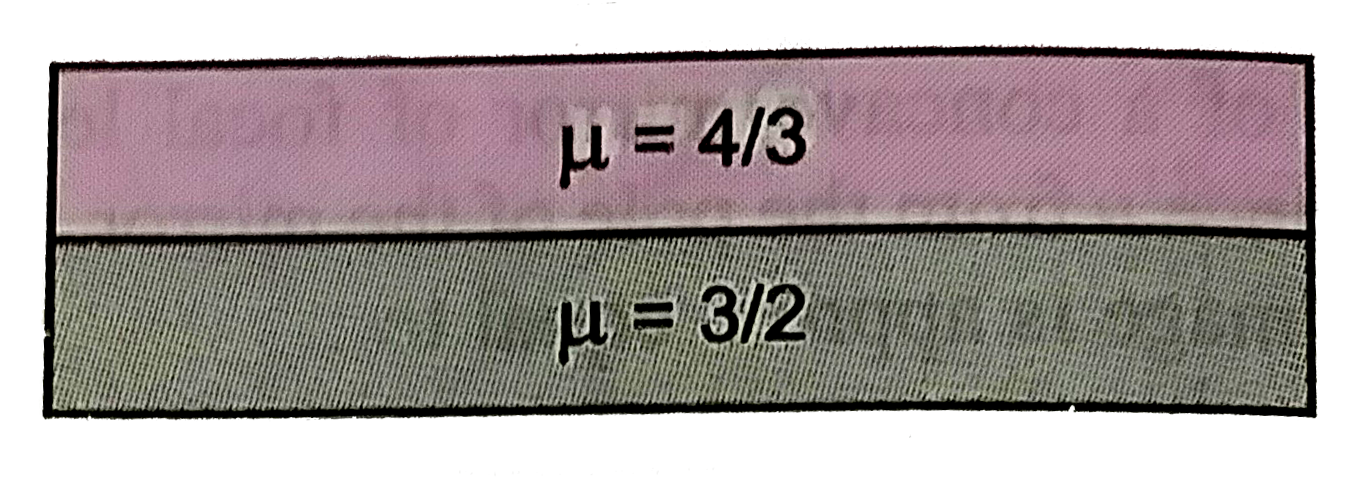 .
.
1.8
1.43
2
None oof the above
The correct Answer is:B
Step by step video & image solution for Considering normal incidence of ray, the equivalent refractive index of combination of two slabs shown in Fig. is. . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View Solution
Knowledge Check
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
A4πdλ(1−1n2sin2θ)1/2+πB4πdλ(1−1n2sin2θ)1/2C4πdλ(1−1n2sin2θ)1/2+π2D4πdλ(1−1n2sin2θ)1/2+2π
When a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5)
View Solution
A ray of light is incident normally on one face of a prism as shown in figure. The refractive index of the material of the prism is 53 and the prism is immersed in water of refractive index 43, then
View SolutionLight incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.
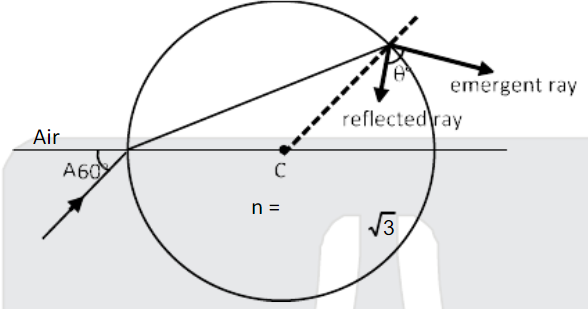
View SolutionConsider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ . The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
View SolutionConsider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
View SolutionA parallel beam of light is incident normally on the flat surface of a hemisphere of radius 6cm and refractive index 1.5, placed in air as shown in figure (i). Assume paraxial ray approxiamtion.
 .
.
View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View Solution
