A particle moves along a curve of unknown shape but magnitude of force F is constant and always acts along tangent to the curve.Then
F many be conservative
F must be conservative
F may be no-conservative
F must be non-conservative
The correct Answer is:D
To solve the problem, we need to analyze the motion of a particle moving along a curve under the influence of a constant force that always acts tangentially to the curve.
1. Understanding the Force:
- The problem states that a particle moves along a curve and the force F is constant in magnitude and always acts along the tangent to the curve at any point.
2. Work Done by the Force:
- The work done W by a force is given by the integral of the force along the path of motion. Since the force is always tangential to the curve, the work done can be expressed as:
W=∫F⋅ds
- Here, ds is the differential displacement along the curve.
3. Calculating Work Done:
- Since the force F is constant in magnitude and always acts along the tangent, we can simplify the expression for work done:
W=F∫ds=F⋅L
- Where L is the total length of the path traveled by the particle.
4. Nature of the Force:
- A conservative force is defined as one where the work done does not depend on the path taken, but only on the initial and final positions. In this case, since the work done depends on the path length L, it indicates that the force is non-conservative.
5. Conclusion:
- Therefore, we conclude that the force acting on the particle is a non-conservative force.
Final Answer:
The correct option is D (the force is non-conservative).
- The problem states that a particle moves along a curve and the force F is constant in magnitude and always acts along the tangent to the curve at any point.
- The work done W by a force is given by the integral of the force along the path of motion. Since the force is always tangential to the curve, the work done can be expressed as:
W=∫F⋅ds
- Here, ds is the differential displacement along the curve.
- Since the force F is constant in magnitude and always acts along the tangent, we can simplify the expression for work done:
W=F∫ds=F⋅L
- Where L is the total length of the path traveled by the particle.
- A conservative force is defined as one where the work done does not depend on the path taken, but only on the initial and final positions. In this case, since the work done depends on the path length L, it indicates that the force is non-conservative.
- Therefore, we conclude that the force acting on the particle is a non-conservative force.
The correct option is D (the force is non-conservative).
Similar Questions
Knowledge Check
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
Aits velocity is constantBits acceleration is constantCits kinetic energy is constantDit moves in a straight line.
A block of mass m is slowly carried on a inclined plane by a force F which always acts along the tangent to the plane. If the co-efficient of friction between the block and incline be μ, then work done by force of friction while carrying block from bottom of the plane to the top will be :
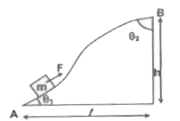
A. dependent on the actual shape of the path between point A and B.
B. will have a total positive value
C. will not change if force F is not applied along the tangent to the plane always.
D. independent of the actual shape of the path between points A and B.
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendiculr to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendiculr to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. It follows that
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View Solution
