In terms of basic units of mass (M), length (L), time (T), and charge (Q), the dimensions of magnetic permeability of vacuum (μ0) would be
[MLQ−2]
[LT−1Q−1]
[ML2T−1Q−2]
[LTQ−1]
The correct Answer is:A
To find the dimensions of magnetic permeability of vacuum (μ0), we can start with the Biot-Savart law, which relates the magnetic field (B) to the current (I) and the distance (R).
1. Start with the Biot-Savart Law:
B=μ0IdlR2
Here, B is the magnetic field, μ0 is the magnetic permeability, I is the current, dl is an infinitesimal length, and R is the distance.
2. Rearranging for μ0:
Rearranging the equation gives:
μ0=BR2Idl
3. Identify the dimensions:
- The dimension of R (length) is (L).
- The dimension of dl (length) is also (L).
- The dimension of current I can be expressed in terms of charge (Q) and time (T) as:
I=QT
4. Substituting dimensions into the equation:
The dimensions of μ0 can now be expressed as:
(μ0)=(B)⋅(L2)(I)⋅(L)
5. Finding the dimensions of the magnetic field B:
From the Lorentz force law:
F=Q⋅V⋅B
Rearranging gives:
B=FQ⋅V
The dimensions of force F are (MLT−2), velocity V is (LT−1), and charge Q is (Q). Therefore:
(B)=(MLT−2)(Q)⋅(LT−1)=(MLT−2)(Q)⋅(L)⋅(T−1)=(M)(Q)⋅(T)
6. Substituting back to find μ0:
Now substituting the dimension of B back into the equation for μ0:
(μ0)=((M)(Q)⋅(T))⋅(L2)(QT)⋅(L)=(M)⋅(L2)(Q)⋅(T)⋅QT⋅(L)
Simplifying this gives:
(μ0)=(M)⋅(L2)(Q2)⋅(T−2)
Which can be rearranged to:
(μ0)=(M)⋅(L)⋅(T2)⋅(Q−2)
7. Final Dimension:
Therefore, the final dimension of magnetic permeability of vacuum (μ0) is:
(μ0)=(MLT−2Q−2)
B=μ0IdlR2
Here, B is the magnetic field, μ0 is the magnetic permeability, I is the current, dl is an infinitesimal length, and R is the distance.
Rearranging the equation gives:
μ0=BR2Idl
- The dimension of R (length) is (L).
- The dimension of dl (length) is also (L).
- The dimension of current I can be expressed in terms of charge (Q) and time (T) as:
I=QT
The dimensions of μ0 can now be expressed as:
(μ0)=(B)⋅(L2)(I)⋅(L)
From the Lorentz force law:
F=Q⋅V⋅B
Rearranging gives:
B=FQ⋅V
The dimensions of force F are (MLT−2), velocity V is (LT−1), and charge Q is (Q). Therefore:
(B)=(MLT−2)(Q)⋅(LT−1)=(MLT−2)(Q)⋅(L)⋅(T−1)=(M)(Q)⋅(T)
Now substituting the dimension of B back into the equation for μ0:
(μ0)=((M)(Q)⋅(T))⋅(L2)(QT)⋅(L)=(M)⋅(L2)(Q)⋅(T)⋅QT⋅(L)
Simplifying this gives:
(μ0)=(M)⋅(L2)(Q2)⋅(T−2)
Which can be rearranged to:
(μ0)=(M)⋅(L)⋅(T2)⋅(Q−2)
Therefore, the final dimension of magnetic permeability of vacuum (μ0) is:
(μ0)=(MLT−2Q−2)
Similar Questions
Using mass (M), length (L), time (T) and current (A) as fundamental quantities, the dimensions of permeability are :
View SolutionUsing mass(M),length(L),time(T) and current(A)as fundamental quantites the demension of permeability is
View SolutionUsing mass (M), length (L), time (T) and current (A) as fundamental quantities, the dimension of permittivity is:
View SolutionUsing mass (M), length (L), time (T) and current (A) as fundamental quantities, the dimension of permittivity is:
View SolutionIf the velocity (V) , acceleration (A) , and force (F) are taken as fundamental quantities instead of mass (M) , length (L),andtime(T) , the dimensions of young's modulus (Y) would be
View SolutionUsing mass (M) , length (L) , time (T) , and electric current (A) as fundamental quantities , the dimensions of permitivity will be
View SolutionMatch the physical quantities given in column I with dimensions expressed interms of mass (M), length (L), time (T) and charge (Q) given in column II and wire the correct answer against the match quantity in labourar form.
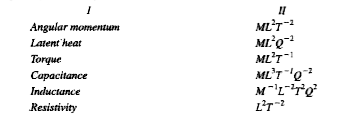
View SolutionThe dimension of B22μ0, where B is magnetic field and μ0 is the magnetic permeability of vacuum, is :
View SolutionThe dimensions of resistivity in terms of M, L, T and Q, where Q stands for the dimensions of charge is
View SolutionLet ε0 denote the dimensional formula of the permittivity of vacuum. If M= mass , L=length , T=time and A=electric current , then dimension of permittivity is given as [MpLqTrAs]. Find the value of p−q+rs
View Solution
