A ball is located in a semicircular trough. The ball is moved slightly to one side and returns to its original locatiun. The ball Is said to be in
neutral equilibrium
unstable equilibrium
stable equilibrium
all of the above.
The correct Answer is:C
To solve the problem, we need to analyze the situation of a ball placed in a semicircular trough and determine the type of equilibrium it exhibits when slightly displaced.
1. Understanding the Setup:
- We have a semicircular trough and a ball resting at the bottom of this trough. The ball is in a stable position due to the shape of the trough.
2. Displacing the Ball:
- When the ball is moved slightly to one side, it is displaced from its original position.
3. Forces Acting on the Ball:
- The gravitational force (mg) acts downward on the ball. When the ball is displaced, there are components of this gravitational force that come into play.
- The component of the gravitational force acting along the direction of the trough will pull the ball back towards the center.
4. Returning to Original Position:
- As the ball is displaced, the restoring force (due to the component of mg acting along the trough) will cause the ball to roll back to its original position.
- If the ball overshoots the center, it will continue to move to the opposite side but will eventually return to the center again.
5. Identifying the Type of Equilibrium:
- Since the ball returns to its original position after being displaced, it indicates that the equilibrium is stable.
- In stable equilibrium, any small displacement results in a restoring force that brings the object back to its original position.
6. Conclusion:
- Therefore, the ball is said to be in stable equilibrium.
Final Answer:
The ball is in stable equilibrium.
- We have a semicircular trough and a ball resting at the bottom of this trough. The ball is in a stable position due to the shape of the trough.
- When the ball is moved slightly to one side, it is displaced from its original position.
- The gravitational force (mg) acts downward on the ball. When the ball is displaced, there are components of this gravitational force that come into play.
- The component of the gravitational force acting along the direction of the trough will pull the ball back towards the center.
- As the ball is displaced, the restoring force (due to the component of mg acting along the trough) will cause the ball to roll back to its original position.
- If the ball overshoots the center, it will continue to move to the opposite side but will eventually return to the center again.
- Since the ball returns to its original position after being displaced, it indicates that the equilibrium is stable.
- In stable equilibrium, any small displacement results in a restoring force that brings the object back to its original position.
- Therefore, the ball is said to be in stable equilibrium.
The ball is in stable equilibrium.
Similar Questions
A ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionAn urn contains 5 red and 2 green balls. A ball is drawn at random from the urn. If the drawn ball is green, then a red ball is added to the urn and if the drawn ball is red, then a green ball is added to the urn, the original ball is not returned to the urn. Now, a second ball is drawn at random from it. The probability that the second ball is red is
View SolutionA ball thrown vertically upward returns to its starting point in 4 s. Find its initial speed.
View SolutionA ball is projected as shown in figure. The ball will return to point:
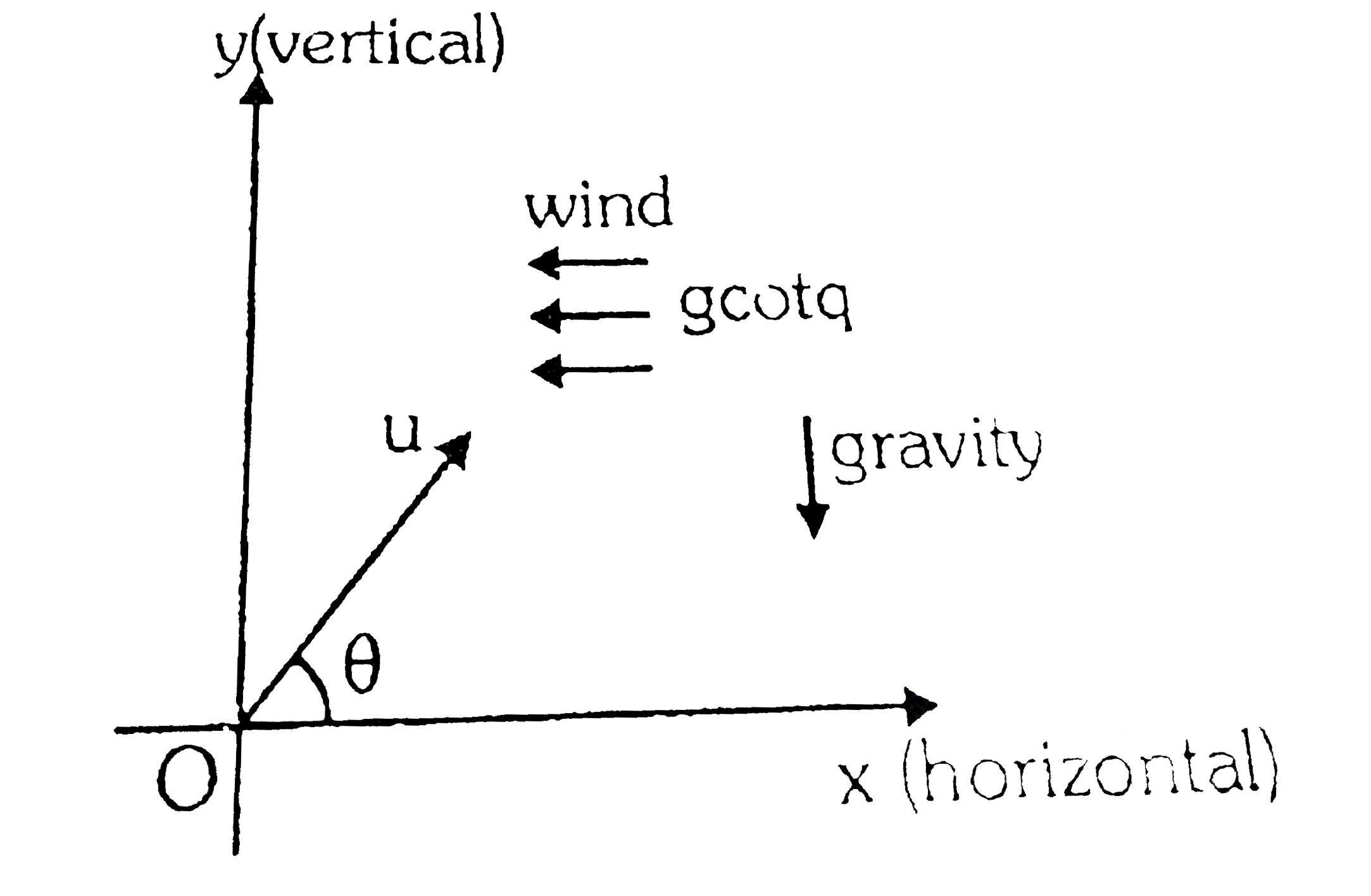
A. O
B. left to point O
C. right to point O
D. none of these
View SolutionSome identical balls are arranged in rows to form an equilateral triangle. The first row consists of one ball, the second row consists of row balls and so on. If 99 more identical balls are added to the total number of balls used in forming the equilateral triangle, then all these balls can be arranged in a square whose each side contains exactly 2 balls less than the number of balls each side of the triangle contains. Then, the number of balls used to form the equilateral triangle is
View SolutionA spherical ball of iron has been melted and made into smaller balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made?
View SolutionA spherical ball of lead has been melted and made in to smaller balls of half the radius of the original one. How many balls can be made?
View SolutionAn iron spherical ball has been melted and recast into smaller balls of equal size. If the radius of each of the smaller balls is 1/4 of the radius of the original ball, how many such balls are made? Compare the surface area, of all the smaller balls combined together with that of the original ball.
View SolutionA spherical ball of lead has been melted and made into identical smaller balls with radius equal to half the radius of the original one. How many such balls can be made ?
View SolutionA bag contans 2017 red balls and 2017 black balls. We remove two balls at a time repeatedly and (1) discard them if they are of some colour (2) discard the black ball and return to the bag the red ball if they are of different colours. Then the probability that this process will terminate with one red ball is 'p' where 3p is______
View Solution
