What is the velocity of the light in the medium if Sin θi=0.707 , Sin θr=0.500 , and the velocity of light in a vacuum is 3.0×108 m/sec ?
2.1×108 m/sec
2.8×108 m/sec
1.4×108 m/sec
4.2×108 m/sec
The correct Answer is:A
To find the velocity of light in a medium given the values of sin(theta_i) and sin(theta_r), we can use Snell's law, which relates the angles of incidence and refraction to the velocities of light in different media.
1. Identify Given Values:
- sinθi=0.707
- sinθr=0.500
- Speed of light in vacuum, c=3.0×108m/s
2. Use Snell's Law:
Snell's law states that:
sinθisinθr=cv
where v is the speed of light in the medium.
3. Rearranging the Equation:
We can rearrange the equation to solve for v:
v=c⋅sinθrsinθi
4. Substituting the Values:
Substitute the known values into the equation:
v=3.0×108⋅0.5000.707
5. Calculating the Ratio:
Calculate the ratio:
0.5000.707≈0.707
6. Final Calculation:
Now, calculate v:
v≈3.0×108⋅0.707≈2.121×108m/s
7. Conclusion:
The velocity of light in the medium is approximately:
v≈2.1×108m/s
- sinθi=0.707
- sinθr=0.500
- Speed of light in vacuum, c=3.0×108m/s
Snell's law states that:
sinθisinθr=cv
where v is the speed of light in the medium.
We can rearrange the equation to solve for v:
v=c⋅sinθrsinθi
Substitute the known values into the equation:
v=3.0×108⋅0.5000.707
Calculate the ratio:
0.5000.707≈0.707
Now, calculate v:
v≈3.0×108⋅0.707≈2.121×108m/s
The velocity of light in the medium is approximately:
v≈2.1×108m/s
Similar Questions
When light is incident on a medium at angle i and refracted into a second medium at an angle r, the graph of sinr versus sini is as shown. From this one can conclude that

(i) the velocity of light in second medium is √3 times the velocity of light in the first medium
(ii) the velocity of light in the first medium is √3 times the velocity of ligth in second medium
(iii) the critical angle of the two media is given by siniC=1√3
(iv) the critical anlge of the two media is given by siniC=1√2
View SolutionIf sinθ=0.5, what is the length of BC ?
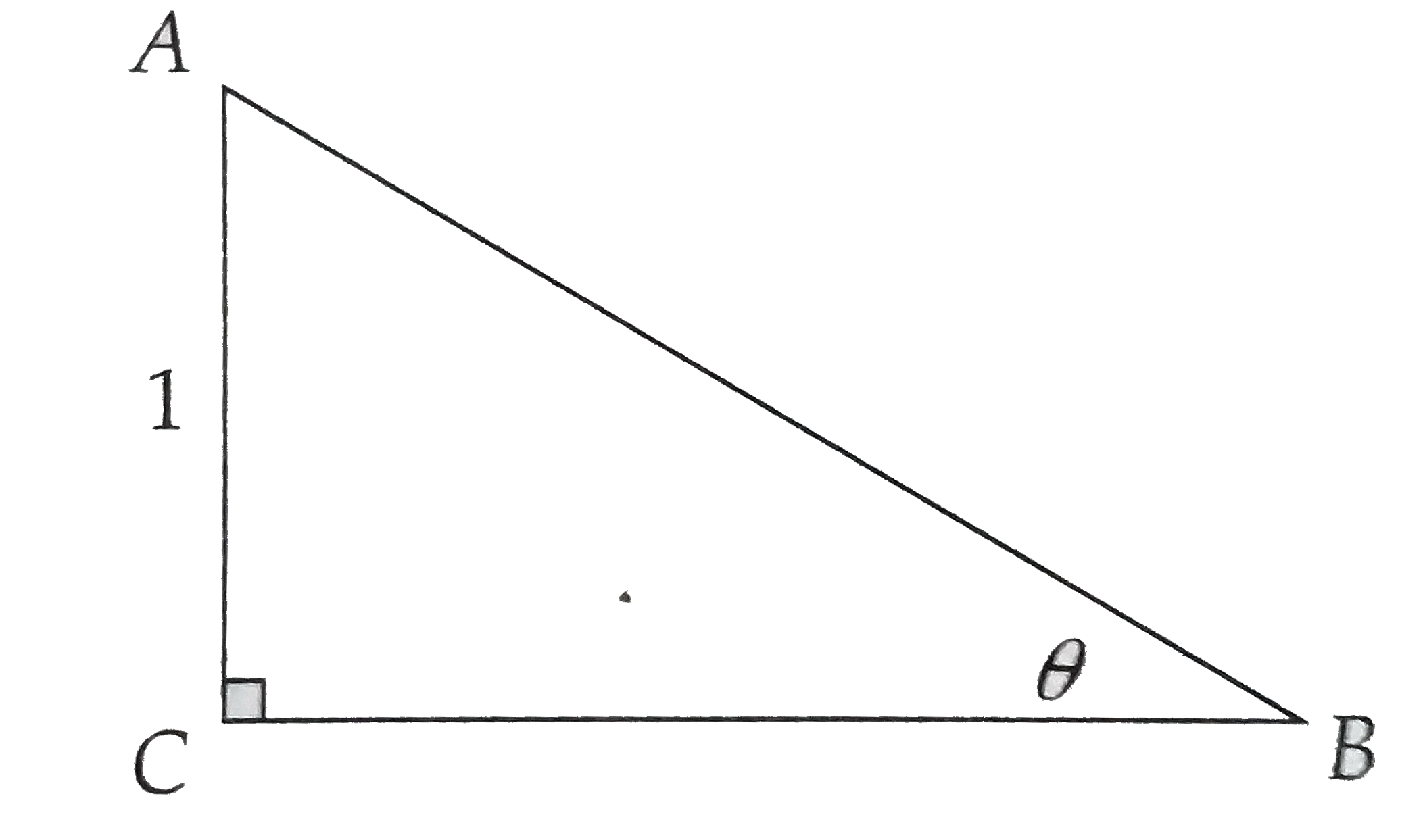
View Solution
Knowledge Check
The angle of minimum deviation for prism of angle π/3isπ/6. Calculate the velocity of light in the material of the prism if the velocity of light in vacuum is 3×108ms−1.
A2.12×108ms−1B1.12×108ms−1C4.12×108ms−1D5.12×108ms−1
sinθ−cosθ=0
View SolutionA ray of light is incident on a medium with angle of incidence I and refracted into a second medium with angle of refraction r. The graph of sin(i)vssin(R) is as shown in figure. Then the velocity of light in the first medium in n times the velocity of light in the second medium. What shoul be th evalue of n?
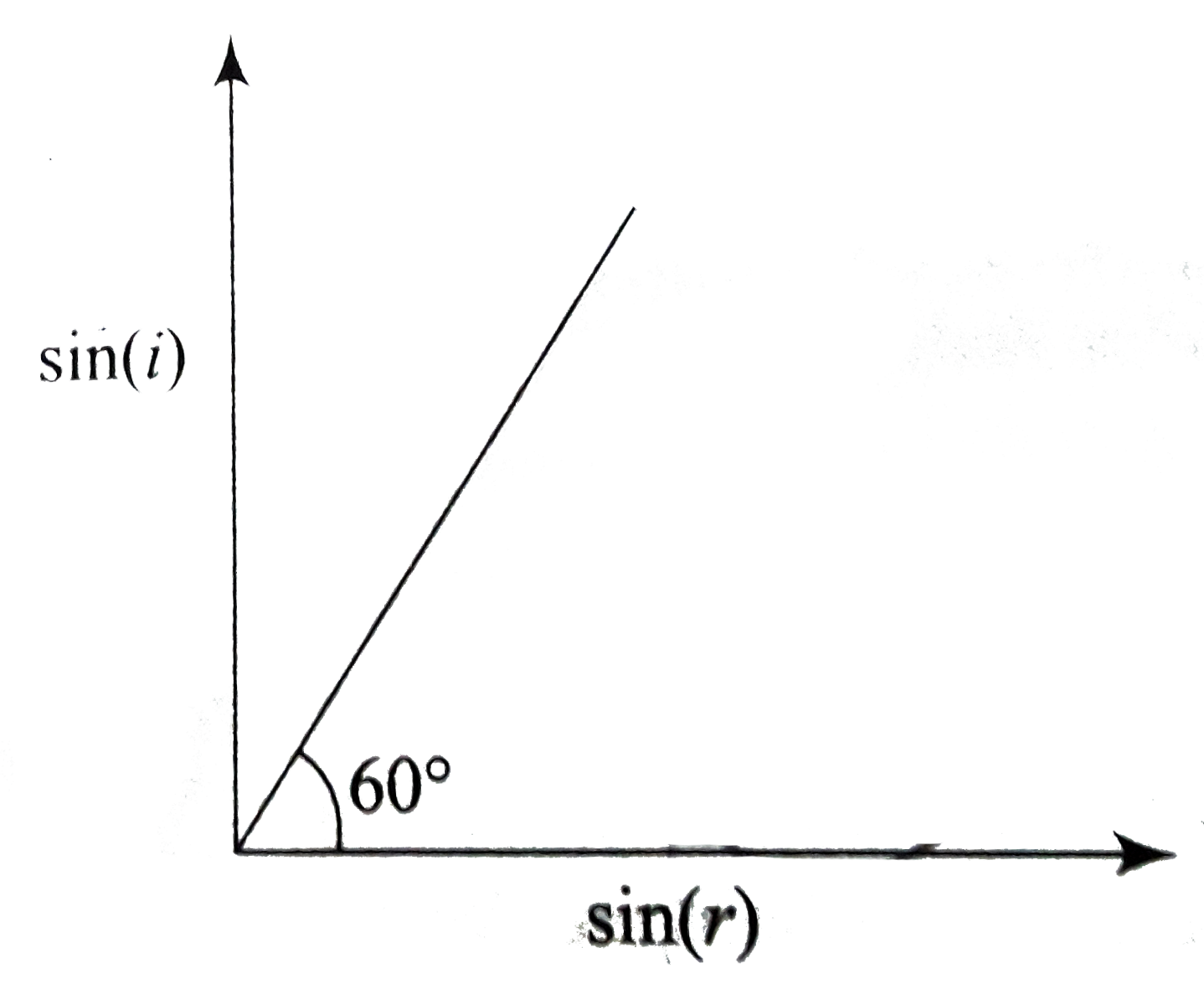
View SolutionIf the refractive index of glass is 1.5. Find the velocity of light in glass. (Velocity of light in vacuum =3×108m/s)
View SolutionThe velocity of light in the core of a step index fibre 2×108m/s and the critical angle at the core-cladding interface is 80∘.Find the numerical aperture and the acceptance angle for the fibre in air.The velocity of light in vacuum is 3×108m/s
View SolutionSolve the general vlaue.
sin7θ+sin4θ+sinθ=0
View SolutionSolve the following equation: sin2theta + sin4theta + sin6theta = 0
View SolutionFind all the value of θ satisfying the equation , sin7θ=sinθ+sin3θ such that 0≤θ≤π
View Solution
