A soap film is formed on a wire ring held vertically and allowed to drain. A diffuse source of while light is observed by reflection in the soap film . In this connection indicate the wrong statement :
The colours are due to refraction of light by the wedge-shaped film
The thickness of the film is of the same order as the wavelength of visible light
The band of colours move downwards as the film drains
Just before the film breaks, it may appear black at the top
The correct Answer is:A
First three statements are correct. The fourth statement alone is wrong, the fringes are due to reflection and interference .
Similar Questions
A soap film in stretched over a reclangular vertical wire frame as shown in the figure, what forces hold section abod in equilibrium ?
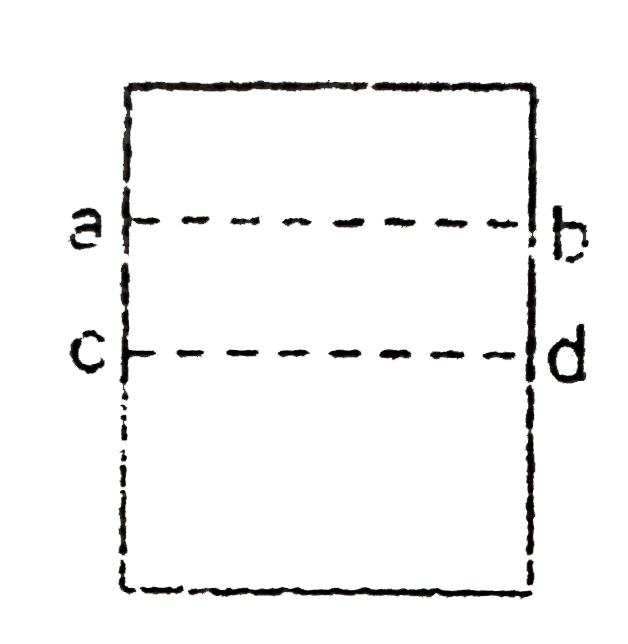
View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View SolutionA : If a thin soap film is arranged vertically the spectrum of coloured fringes are spread equally on the film.
R : The colours of the film is dependent on the thickness of film and wavelength of the light.
View SolutionThin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.
Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.
III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
The average human eye sees colors with wavelength between 430 nm to 680 nm. For what visible wavelength (s) will a 350 nm thick (n=1.35) soap film produce maximum destructive interference?
View SolutionA soap film is on a rectangular wire ring of size 2 cm × 3 cm. If the size of the film is changed to 3 cm × 3 cm, calculate the work done in this process. (The surface tension of soap solution is 3.0×10−2Nm−1).
View Solution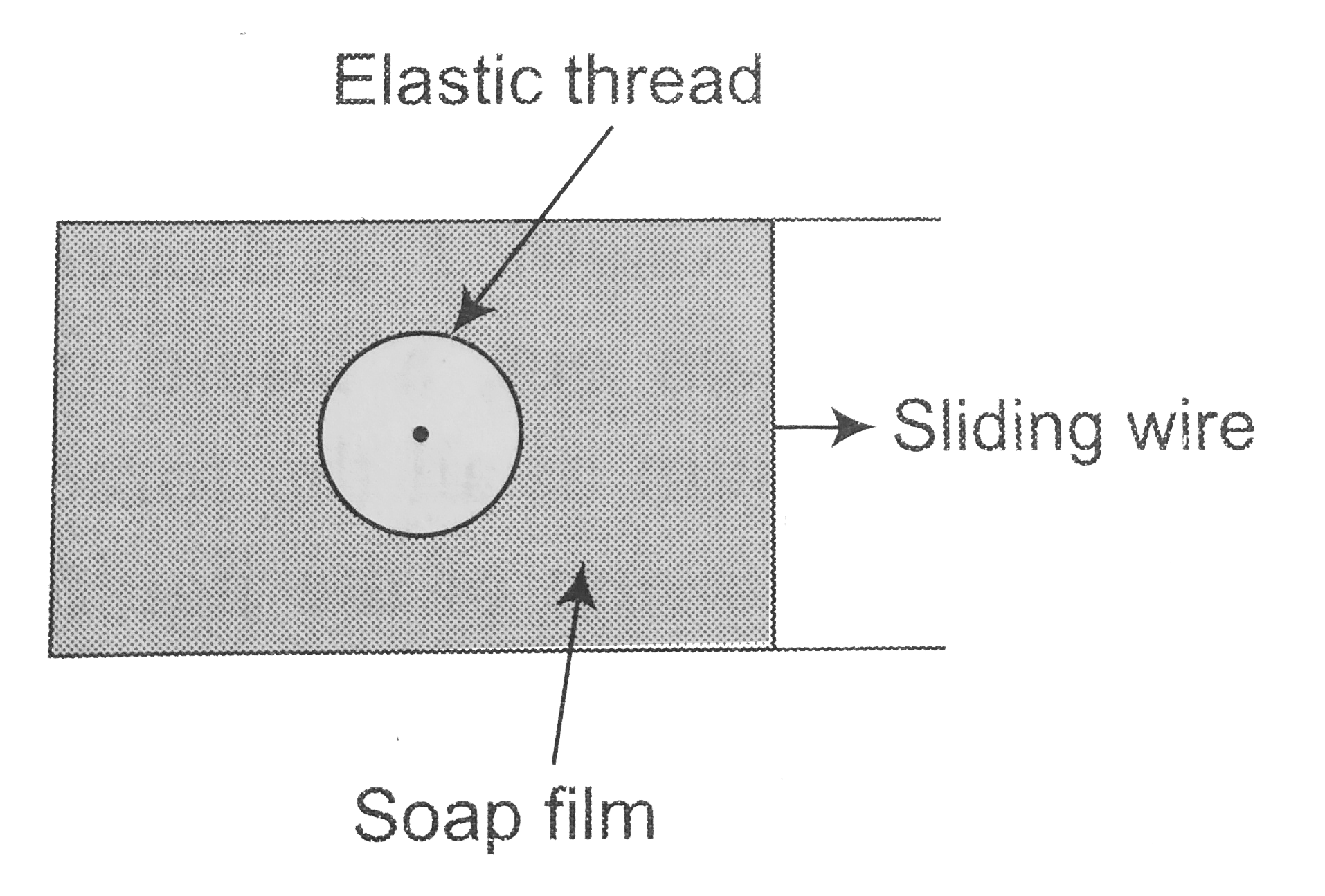
The figure shows a soap film in which a closed elastic thread is lying. The film inside the thread is pricked. Now the sliding wire is moved out so that the surface area increases. The radius circle of the circle formed by elastic thread will
View SolutionA wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
View SolutionA wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm long thread is gently put on the film and the film is pricked with a needle inside the loop. The thread loop takes the shape of a circle. Find the tension in the thread. Surface tension of soap solution =0.030Nm−1.
View SolutionA U-shaped wire is dipped in a soap solution, and removed. A thin soap film formed between the wire and a light slider supports a weight of 1.5×10−2N (which includes the small weigh of the slider). The length of the slider is 30cm. What is the surface tension of the film?
View Solution


