In which case there is maximum extension in the wire, if same force is applied on each wire
A. L=400 cm, d=0.01 mm
B. L=300 cm, d=0.03 mm
C. L=200 cm, d=0.02 mm
D. L=500 cm, d=0.05 mm
L=400 cm, d=0.01 mm
L=300 cm, d=0.03 mm
L=200 cm, d=0.02 mm
L=500 cm, d=0.05 mm
The correct Answer is:A
To determine which wire experiences the maximum extension when the same force is applied to each wire, we can use the formula derived from Young's modulus of elasticity. The extension (l) in the wire can be expressed as:
l=F⋅LY⋅A
Where:
- l = extension in the wire
- F = force applied
- L = original length of the wire
- Y = Young's modulus of the material
- A = cross-sectional area of the wire
The cross-sectional area A can be expressed in terms of the diameter d of the wire as:
A=πd24
Substituting this into the extension formula gives:
l=F⋅LY⋅(πd24)=4F⋅LY⋅πd2
From this equation, we can see that the extension l is directly proportional to the ratio Ld2:
l∝Ld2
Now, we need to evaluate the ratio Ld2 for each option provided:
1. Option A: L=400cm,d=0.01mm=0.001cm
Ld2=400(0.001)2=4000.000001=400000000
2. Option B: L=300cm,d=0.03mm=0.003cm
Ld2=300(0.003)2=3000.000009=33333333.33
3. Option C: L=200cm,d=0.02mm=0.002cm
Ld2=200(0.002)2=2000.000004=50000000
4. Option D: L=500cm,d=0.05mm=0.005cm
Ld2=500(0.005)2=5000.000025=20000000
Now, we can compare the values of Ld2:
- Option A: 400000000
- Option B: 33333333.33
- Option C: 50000000
- Option D: 20000000
The maximum value of Ld2 is for Option A, which means that Option A will have the maximum extension in the wire.
Final Answer:
Option A has the maximum extension in the wire.
- l = extension in the wire
- F = force applied
- L = original length of the wire
- Y = Young's modulus of the material
- A = cross-sectional area of the wire
Ld2=400(0.001)2=4000.000001=400000000
Ld2=300(0.003)2=3000.000009=33333333.33
Ld2=200(0.002)2=2000.000004=50000000
Ld2=500(0.005)2=5000.000025=20000000
- Option B: 33333333.33
- Option C: 50000000
- Option D: 20000000
Option A has the maximum extension in the wire.
Similar Questions
A cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
View SolutionThe length of a rod is measured by four different instruments and the measurements are reported as
A. 500.0 mm , B. 50.0 cm , C.0.500 m , D. 5.0×10−4 km
We can conclude that
View Solution1cm is equal to: (a) 0.1m (b) 0.01m (c) 0.10m (d) 0.001m
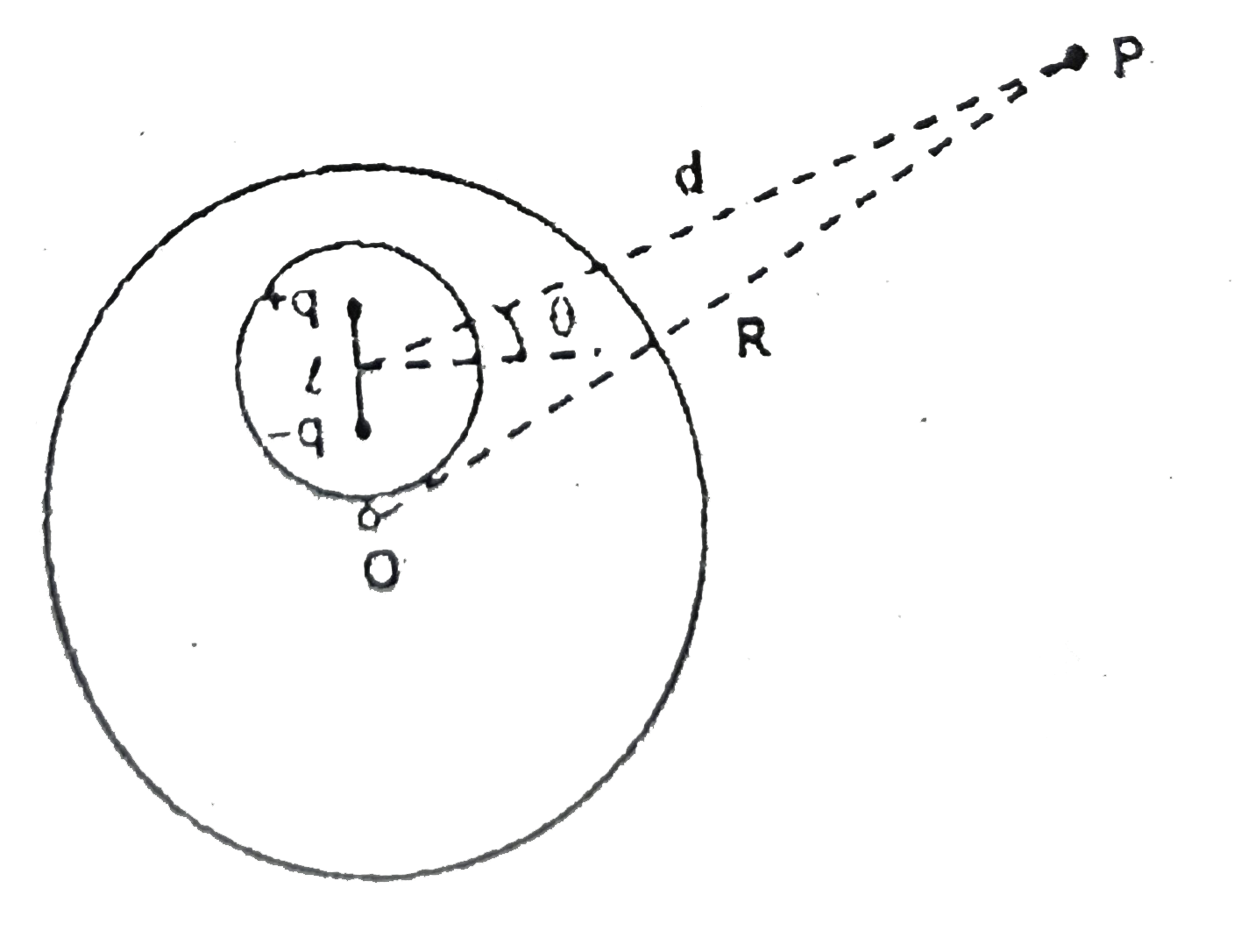
View SolutionA cavity is taken out from a uniform conducting sphere. Inside the cavity a dipole is placed as shown in the figure. Find the potential at point P (in Volt).
(q=10−8C, l=0.1mm, θ=30∘, d=10cm, R=12cm)
View SolutionThe relative error in resistivity of a material where
resistance = 1.05 + 0.01 W
diameter = 0.60 + 0.01 mm
length = 75.3 + 0.1 cm is
View SolutionConvert the as direct.
0.5 sq. cm into sq. mm
View SolutionIn Figure, if lines l and m are parallel lines, then x=
(a)700
(b) 1000
(c) 400
(d) 300
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionIf L = 2.06 cm ±0.02cm,B=1.11cm±0.03cm. What are (L+B) and (L-B) equal to ?
View Solution
