The correct relation is
ΔG−RT ln K/Q
ΔG=−RT ln K
ΔG=−RT ln Q/K
ΔG=+RT ln Q
The correct Answer is:A
To solve the question regarding the correct relation involving Gibbs free energy change (ΔG), we will follow these steps:
1. Understanding Gibbs Free Energy Change:
- The Gibbs free energy change (ΔG) indicates the spontaneity of a reaction. If ΔG is negative, the reaction is spontaneous; if positive, it is non-spontaneous.
2. Standard Gibbs Free Energy Change:
- The standard Gibbs free energy change (ΔG°) is defined for reactions under standard conditions (1 bar pressure, 1 M concentration). It can be calculated using the formula:
ΔG°=−RTlnK
where R is the universal gas constant, T is the temperature in Kelvin, and K is the equilibrium constant.
3. Gibbs Free Energy Change for Non-Standard Conditions:
- For reactions that are not at equilibrium, the Gibbs free energy change is given by:
ΔG=ΔG°+RTlnQ
where Q is the reaction quotient, which reflects the current concentrations of reactants and products.
4. Combining the Equations:
- We can substitute the expression for ΔG° into the equation for ΔG:
ΔG=−RTlnK+RTlnQ
- This can be rearranged to:
ΔG=RT(lnQ−lnK)=RTln(QK)
5. Identifying the Correct Relation:
- From the derived equation, we see that ΔG is related to the ratio of the reaction quotient to the equilibrium constant:
ΔG=RTln(QK)
- Therefore, the correct relation among the given options is likely to be the one that matches this derived equation.
Conclusion:
- Based on the analysis, the correct answer is Option C, which corresponds to the relation we derived.
- The Gibbs free energy change (ΔG) indicates the spontaneity of a reaction. If ΔG is negative, the reaction is spontaneous; if positive, it is non-spontaneous.
- The standard Gibbs free energy change (ΔG°) is defined for reactions under standard conditions (1 bar pressure, 1 M concentration). It can be calculated using the formula:
ΔG°=−RTlnK
where R is the universal gas constant, T is the temperature in Kelvin, and K is the equilibrium constant.
- For reactions that are not at equilibrium, the Gibbs free energy change is given by:
ΔG=ΔG°+RTlnQ
where Q is the reaction quotient, which reflects the current concentrations of reactants and products.
- We can substitute the expression for ΔG° into the equation for ΔG:
ΔG=−RTlnK+RTlnQ
- This can be rearranged to:
ΔG=RT(lnQ−lnK)=RTln(QK)
- From the derived equation, we see that ΔG is related to the ratio of the reaction quotient to the equilibrium constant:
ΔG=RTln(QK)
- Therefore, the correct relation among the given options is likely to be the one that matches this derived equation.
- Based on the analysis, the correct answer is Option C, which corresponds to the relation we derived.
Similar Questions
Knowledge Check
The correct relation for speed is :
ASpeed = distance x timeBSpeed = distance/timeCSpeed = time/distanceDSpeed = 1/(distance x time)The correct relation between joule and erg is
A1J=10−5 ergB1J=105 ergC1J=10−7 ergD1J=107 ergThe correct relation between linear velocity →v and angular velocity →ω of a particle is
A→v=→r×→ωB→v=→ω×→rC→ω=→r×→vD→ω=→v×→r
The correct relation between limit of resolution and resolving power is
View SolutionThe correct relation between compound(s) I and II is/are
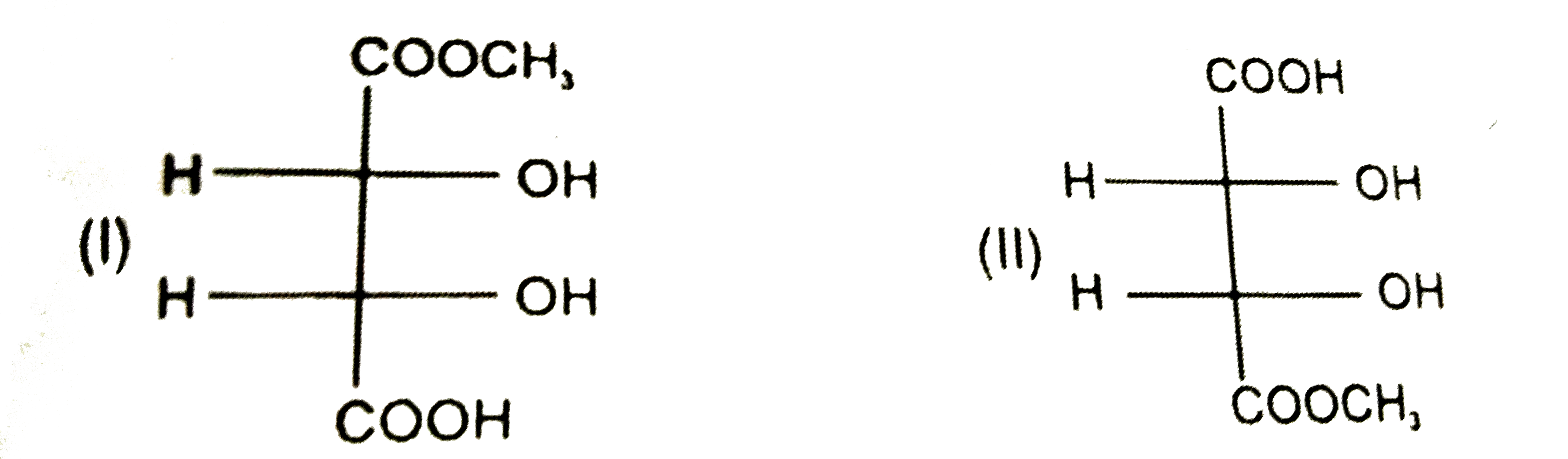
View SolutionThe correct relation for radius of atom and edge - length in case of fcc arrangement is
View SolutionTwo bulbs of (40 W, 200 V) and (100 W, 200 V). Then correct relation for their resistance:
View SolutionThe correct relation between tav=average life and t1/2= half life for a radioactive nuclei.
View Solution
