Distance between sun and earth is 2×108 km, temperature of sun 6000 K, radius of sun 7×105 km, if emmisivity of earth is 0.6 , then find out temperature of earth in thermal equilibrium.
400 K
300 K
500 K
600 K
The correct Answer is:B
For thermal equilibrium
energy received by earth = Energy emmited by earth
T4s×R2s4×d2×e=T4e
⇒(6000)4×(7×108)24×(2×1011)2×0.6=T4e
⇒36×36×7×74×4×0.6×106=T4e
⇒66.15×108=T4e
Te=300K
Similar Questions
If temperature of Sun=6000K, radius of Sun is 7.2×105Km, radius of earth=6000 Km & distance
between earth and Sun=15×107Km. find intensity of light on earth.View SolutionLet us assume that sun radiates like a black body with surface temperature at T0=6000K and earth absorbs radiation coming from sun only. If both earth and sun are considered perfect spheres with distance between centre of earth and centre of sun to be 200 times the radius of sun, find the temperature (in Kelvin) of surface of earth in steady state (assume radiation incident on earth to be almost parallel).
View Solution
Knowledge Check
- Question 1 - Select One
If the earth is a point mass of 6×1024 kg revolving around the sun at a distance of 1.5×108 km and in time T=3.14×107 s, then the angular momentum of the earth around the sun is
A1.2×1018kgm2/sB1.8×1029kgm2/sC1.5×1037kgm2/sD2.7×1040kgm2/s - Question 2 - Select One
The earth receives its surface radiation from the sun at the rate of 1400 W/m2. The distance of the centre of the sun from the surface of the earth is 1.5×1011 m and the radius of the sun is 7.0×108 m. Treating sun as a black body, it follows from the above data that its surface temeperature is
A5810 KB106 KC50.1 KD5801∘C
The Earth and Jupiter are two planets of the sun. The orbital radius of the earth is 107m and that of Jupiter is 4×107m If the time period of revolution of earth is T=365 days find time period of revolution of the Jupiter
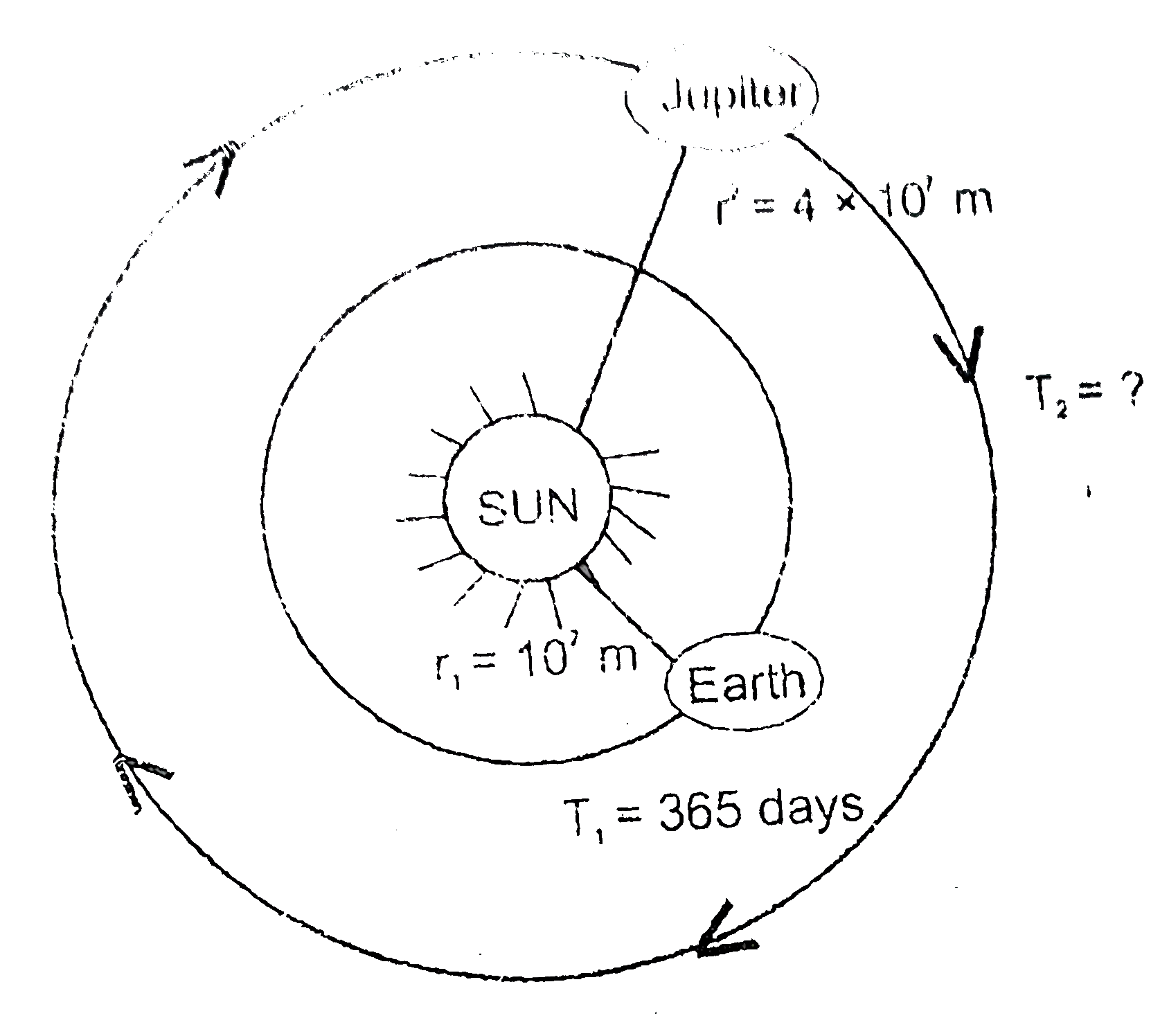 .View Solution
.View SolutionIf the earth is a point mass of 6×1024kg revolving around the sun at a distance of 1.5×108km and in time, T=3.14×107s, then the angular momentum of the earth around the sun is
View SolutionA rocket is launched normal to the surface of the earth, away from the sun, along the line joining the sun and the earth. The sun is 3×105 times heavier than the earth and is at a distance 2.5×104 times larger than the radius of the earth. the escape velocity from earth's gravitational field is ue=11.2kms−1. The minmum initial velocity (ue)=11.2kms−1. the minimum initial velocity (us) required for the rocket to be able to leave the sun-earth system is closest to (Ignore the rotation of the earth and the presence of any other planet
View SolutionThe intensity of solar radiation just outside the earth's atmosphere is measured to be 1.4kW/m2. If the radius of the sun 7×108m, while the earth-sun distance is 150×106km, then find
i. the intensity of salr radiation at the surface of the sun.
ii. the temperature at the surface of the sun assuming it to be a black body,
iii. the most probable wavelength in solar radiation.View SolutionThe mass of the earth is 6×1024 kg and that of the moon is7.4×1022 kg. If the distance between the earth and the moon is 3.84×105 km, calculate the force exerted by the earth on the moon. (Take G =6.7×10–11Nm2kg−2)
View SolutionIf the distance between the sun and the earth is increased by three times, then attraction between two will
View Solution
