1 mole of a diatomic is heated through isochoric process from 300 k to 500 K. The entropy is :
10.61
38.26
20.05
30
The correct Answer is:A
To solve the problem of finding the entropy change (ΔS) for 1 mole of a diatomic gas heated through an isochoric process from 300 K to 500 K, we can follow these steps:
Step 1: Understand the process
In an isochoric process, the volume remains constant. The formula for the change in entropy (ΔS) for an ideal gas during an isochoric process is given by:
ΔS=nCvln(T2T1)
where:
- n = number of moles
- Cv = molar heat capacity at constant volume
- T1 = initial temperature
- T2 = final temperature
Step 2: Identify the values
From the question:
- n=1 mole
- T1=300K
- T2=500K
For a diatomic gas, the molar heat capacity at constant volume (Cv) is:
Cv=52R
where R (the universal gas constant) is approximately 8.314J/(mol⋅K).
Step 3: Calculate Cv
Substituting the value of R:
Cv=52×8.314=20.785J/(mol⋅K)
Step 4: Substitute values into the entropy formula
Now we can substitute the values into the entropy change formula:
ΔS=1×20.785ln(500300)
Step 5: Calculate the logarithm
Calculating the ratio:
500300=53
Now, calculate the natural logarithm:
ln(53)=ln5−ln3
Using approximate values:
ln5≈1.6094andln3≈1.0986
Thus,
ln(53)≈1.6094−1.0986=0.5108
Step 6: Final calculation of ΔS
Now substitute back into the equation for ΔS:
ΔS≈20.785×0.5108≈10.61J/K
Conclusion
The change in entropy (ΔS) for the process is approximately:
ΔS≈10.61J/K
In an isochoric process, the volume remains constant. The formula for the change in entropy (ΔS) for an ideal gas during an isochoric process is given by:
- n = number of moles
- Cv = molar heat capacity at constant volume
- T1 = initial temperature
- T2 = final temperature
From the question:
- n=1 mole
- T1=300K
- T2=500K
Substituting the value of R:
Now we can substitute the values into the entropy change formula:
Calculating the ratio:
Now substitute back into the equation for ΔS:
The change in entropy (ΔS) for the process is approximately:
Similar Questions
One mole of ideal monatomic gas was taken through isochoric heating from 100 K to 1000 K. Calculate ΔSsystem,Δsurr and ΔStotal in
(i) When the process carried out reversibly (ii) When the process carried out irreversibly (one step)
View SolutionOne mole of Ideal monatomic gas taken through Isochoric heating for 100K to 1000K then correct Match is
View SolutionWhen 1.5 mol of a gas is heated at constant volume from 300 K to 350 K and the heat supplied to the gas is 750 J then the correct option is
View SolutionOne mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionIn figure, a sample of 3 moles of an ideal gas is undergoing through a cyclic process ABCA.A total of 1500J of heat is withdraw from the sample in the process. The work done by the gas during the part BC is −PKJ.FINDP.(R=253J/moleK)

View SolutionCalculate ΔS for 3 mole of a diatomic ideal gas which is heated and compressed from 298 K and 1 bar to 596 K and 4 bar: [Given: Cv,m(gas)=52R,ln(2)=0.70,R=2calK−1mol−1]
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
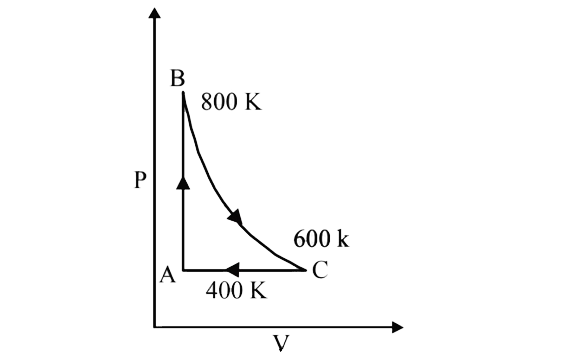
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:

View SolutionWhen 3.0 mole of an ideal diatomic gas is heated and compressed simultaneously from 300K, 1.0 atm to 400K and 5.0atm, the change in entropy is (Use CP=72R for the gas)
View SolutionAt constant volume , 4 moles of an ideal gas when heated from 300 K to 500 K change its internal energy by 5000 J. The molar heat capacity at constant volume is ?
View Solution
