A disc of radius 5 m is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
2cm
3cm
4 cm
6cm
The correct Answer is:C
To solve the problem step by step, we need to determine the maximum distance from the axis of the rotating disc where the block can be placed without sliding off due to the centrifugal force acting on it.
Step 1: Understanding the Forces
When the block is placed on the rotating disc, it experiences a centrifugal force due to the rotation. This force tries to push the block outward. The frictional force between the block and the disc must be sufficient to keep the block from sliding off.
Step 2: Setting Up the Equation
The maximum frictional force Ff that can act on the block is given by:
Ff=μk⋅m⋅g
where:
- μk=0.4 (coefficient of kinetic friction),
- m=2kg (mass of the block),
- g=9.8m/s2 (acceleration due to gravity).
The centrifugal force Fc acting on the block when it is at a distance x from the axis is given by:
Fc=m⋅ω2⋅x
where ω=10rad/s (angular frequency).
Step 3: Equating Forces
For the block to not slide off, the frictional force must be equal to or greater than the centrifugal force:
μk⋅m⋅g≥m⋅ω2⋅x
We can simplify this by canceling m from both sides (assuming m≠0):
μk⋅g≥ω2⋅x
Step 4: Solving for x
Rearranging the equation to solve for x:
x≤μk⋅gω2
Step 5: Substituting Values
Now, substituting the known values into the equation:
x≤0.4⋅9.8102
Calculating the right-hand side:
x≤3.92100=0.0392m
Converting to centimeters:
x≤3.92cm
Step 6: Conclusion
The maximum distance from the axis where the block can be placed without sliding is approximately 3.92cm.
When the block is placed on the rotating disc, it experiences a centrifugal force due to the rotation. This force tries to push the block outward. The frictional force between the block and the disc must be sufficient to keep the block from sliding off.
The maximum frictional force Ff that can act on the block is given by:
Ff=μk⋅m⋅g
where:
- μk=0.4 (coefficient of kinetic friction),
- m=2kg (mass of the block),
- g=9.8m/s2 (acceleration due to gravity).
Fc=m⋅ω2⋅x
where ω=10rad/s (angular frequency).
For the block to not slide off, the frictional force must be equal to or greater than the centrifugal force:
μk⋅m⋅g≥m⋅ω2⋅x
We can simplify this by canceling m from both sides (assuming m≠0):
μk⋅g≥ω2⋅x
Rearranging the equation to solve for x:
x≤μk⋅gω2
Now, substituting the known values into the equation:
x≤0.4⋅9.8102
Calculating the right-hand side:
x≤3.92100=0.0392m
Converting to centimeters:
x≤3.92cm
The maximum distance from the axis where the block can be placed without sliding is approximately 3.92cm.
Similar Questions
A disc of mass 1 kg and radius 0.1 m is rotating with angular velocity 20 rad/s. What is angular velocity (in rad/s) if a mass of 0.5 kg is put on the circumference of the disc ?
View SolutionA disc of mass 2 kg and radius 0.2 m is rotating with angular velocity 30rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc ?
View SolutionA disc of radius R=2m starts rotating wth constant angular acceleration α=(2rad)/s2. A block of mass m=2kg is kept at a distance R2 from the centre of disc. The coeffiecient of friction between disc and block is μs=0.4,μk=0.3. Acceleration of block when it just slips w.r.t. ground and w.r.t. disc are respectively−(g=10ms−2)
View SolutionA disc of mass 1 kg and radius 0.1 m is rotating with angular velocity 20 rad s−1. What is angular velocity, if a mass of 0.25 kg is put on periphery of the disc?
View SolutionA disc of radius 4 m is rotating about its fixed center with a constant angular velocity ω = 2 rad /s ( in the horizontal plane.) A bloc s also rotating with disc without slippng . If co- efficient of friction between the bloc and the disc is 0⋅4 then the maximum distance at which the block can rotate without slipping s ( g = 10m/s2) brgt
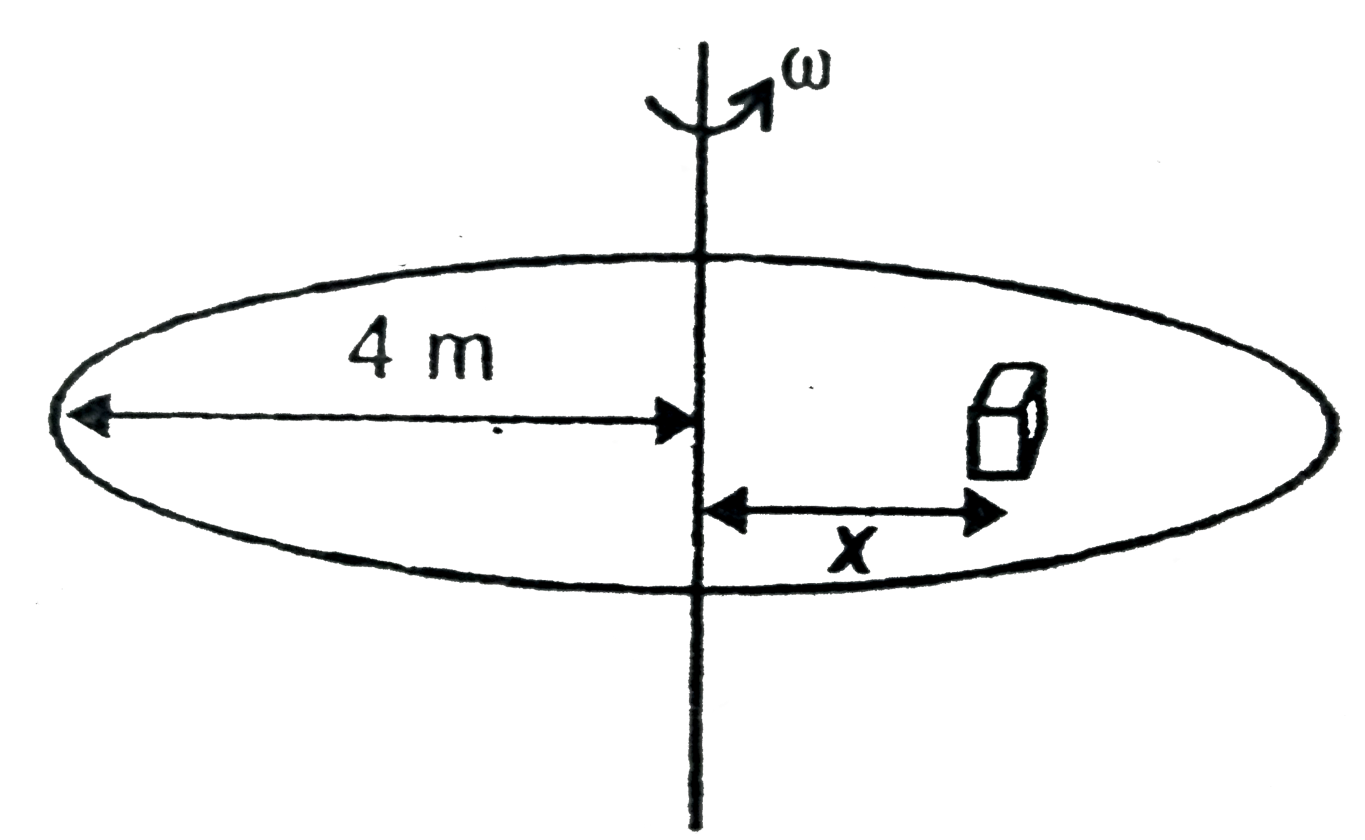
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
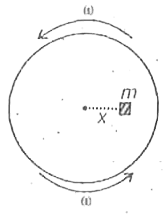
View SolutionA copper disc of radius 1 m is rotated about its natural axis with an angular velocity 2 rad/sec in a uniform magnetic field of 5 tesla with its plane perpendicular to the field. Find the emf induced between the centre of the disc and its rim.
View SolutionA block of mass m = 20 kg is kept is a distance R = 1m from central axis of rotation of a round turn table (A table whose surface can rotate about central axis). Table starts from rest and rotates with constant angular acceleration, α=3rad/sec2. The friction coefficient between block and table is μ=0.5. At time t=x30 from starting of motion (i.e. t =0) the block is just about to slip. Find the value of x (g=10m/s2)
View Solution
