α particle is revolving in radius r with frequency f then find value of magnetic dipole moment .
2evr
evr
3evr
4evr
The correct Answer is:B
To find the magnetic dipole moment of an alpha particle revolving in a circular path of radius r with frequency f, we can follow these steps:
1. Identify the Charge of the Alpha Particle:
An alpha particle consists of 2 protons and 2 neutrons, hence it has a charge of 2e, where e is the elementary charge (e≈1.6×10−19 C).
2. Determine the Current:
The current I due to the revolving charge can be defined as the charge passing a point per unit time. The time period T for one complete revolution is given by:
T=1f
Therefore, the current I can be expressed as:
I=ChargeTime period=2eT=2ef
3. Calculate the Area of the Circular Path:
The area A of the circular path with radius r is given by:
A=πr2
4. Calculate the Magnetic Dipole Moment:
The magnetic dipole moment μ is given by the product of the current and the area:
μ=I⋅A
Substituting the expressions for I and A:
μ=(2ef)⋅(πr2)
Thus, we have:
μ=2efπr2
5. Final Expression:
We can simplify the expression to focus on the terms relevant to the magnetic dipole moment:
μ=ef⋅(2πr2)
Conclusion:
The magnetic dipole moment μ of the alpha particle revolving in a circular path of radius r with frequency f is given by:
μ=ef⋅(2πr2)
An alpha particle consists of 2 protons and 2 neutrons, hence it has a charge of 2e, where e is the elementary charge (e≈1.6×10−19 C).
The current I due to the revolving charge can be defined as the charge passing a point per unit time. The time period T for one complete revolution is given by:
T=1f
Therefore, the current I can be expressed as:
I=ChargeTime period=2eT=2ef
The area A of the circular path with radius r is given by:
A=πr2
The magnetic dipole moment μ is given by the product of the current and the area:
μ=I⋅A
Substituting the expressions for I and A:
μ=(2ef)⋅(πr2)
Thus, we have:
μ=2efπr2
We can simplify the expression to focus on the terms relevant to the magnetic dipole moment:
μ=ef⋅(2πr2)
The magnetic dipole moment μ of the alpha particle revolving in a circular path of radius r with frequency f is given by:
μ=ef⋅(2πr2)
Similar Questions
Knowledge Check
Which does not have zero value of dipole moment?
A[Ni(CN)4]2−BCHCl3CCO2DNH3An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
Aeh4πmBeh2πmCeh24πmDe2h4πm
A particle of charge 'q' and mass 'm' move in a circular orbit of radius 'r' with frequency 'v' the ratio of the magnetic moment to angular momentum is:
View SolutionA charged particle (charge q) is moving in a circle of radius R with unifrom speed v. The associated magnetic moment μ is given by
View SolutionIf an electron revolves around a nucleus in a circular orbit of radius R with frequency n, then the magnetic field produced at the center of the nucleus will be
View Solution(a) Write the expression for the equivalent megnetic moment of a planer current loop of area A, having N turns and carrying a current i. Use the expression to find the magentic dipole moment of a revolving electron ?
(b) A circuit loop of radius r, having N turns and carrying current I, is kept in the XY plane. It is then subjected to a uniform magnetic field →B=Bxˆi+Byˆj+Bzˆk . Obtain expression for the magnetic potential energy of the coil-magnetic field system.
View SolutionA circular coil of Radius R is folded across its diameter such that the planes of two half rings are perpendicular to each other as shown in the figure. If the current through the coil is calculate the magnetic dipole moment of the configuration so formed.
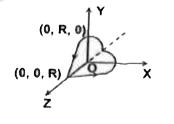
View SolutionFollowing figures show the arrangement of bar magnets in different configurations. Each magnet has magnetic dipole moment (m). Which configuration has highest value of magnetic dipole moment?
View Solution

