Question

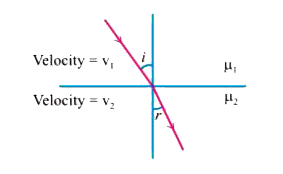
$\frac{\sin i}{\sin r}$ relation was given by …………

Options

A. newton
B. raman
C. snell
D. faraday

Explanation

To solve the question regarding the relation $$\frac{\sin i}{\sin r}$$, we will follow these steps:

1. Understanding the Relation:
- The relation \( \frac{\sin i}{\sin r} \) is associated with the angles of incidence (\( i \)) and refraction (\( r \)) when light passes from one medium to another.

2. Definition of Terms:
- \( \sin i \) refers to the sine of the angle of incidence.
- \( \sin r \) refers to the sine of the angle of refraction.
- This ratio is used to define the refractive index (\( \mu \)) of a medium.

3. Refractive Index:
- The refractive index (\( \mu \)) is defined as the ratio of the sine of the angle of incidence to the sine of the angle of refraction:
\( \mu = \frac{\sin i}{\sin r} \)

4. Identifying the Scientist:
- The question asks who formulated this relation. The correct scientist associated with this law is Arsenal (often referred to as Snell's Law).

5. Conclusion:
- Therefore, the correct answer to the question is option number three: Arsenal.