In the expression buoyant force or upthrust =V×ρ×gρ is the density of the liquid displaced.
1
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - CONCEPT APPLICATION (LEVEL 2)20videos
HYDROSTATICS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - CONCEPT APPLICATION (LEVEL 3)10videos
HYDROSTATICS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - TEST YOUR CONCEPTS (ESSAY TYPE QUESTION)4videos
HYDROSTATICS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HEATEXERCISE - CONCEPT APPLICATION Level 310videos
HEAT
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICS EXERCISE - CONCEPT APPLICATION (Level 3) (Application Based Questions )5videos
KINEMATICS
Similar Questions
What causes buoyant force (or upthrust) on a boat ?
View SolutionIn Fig. , a rectangular block floats in a liquid . A block of mass m = 0.500 kg and density ρ=700kg/m3 floats face down in a liquid of density ρf=1200kg/m3 . What are the magnitude of the buoyant force on the block from the liquid , the weight of the liquid displaced by the block (liquid that would be in the space now occupied by the block ) , and the mass of that displaced liquid ? What fraction of the block's volume is submerged ? What fraction of its height is submerged ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
According to Archimedes's principle the loss in of weight is equal to (V is the volume displaced by the body, ρ is the density of liquid in which body is immersed)
AVρgB2VρgCVρg2DVρg4 - Question 2 - Select One
An object with uniform density ρ is attached to a spring that is known to stretch linearly with applied force as shown below.
When the spring-object system is immersed in a liquid of density ρ1 as shown in the figure, the spring stretches by an amount x1(ρ>ρ1). When the experiment is repeated in a liquid of density ρ2>ρ1, the spring stretches by an amount x2. Neglecting any buoyant force on the spring, the density of the object is
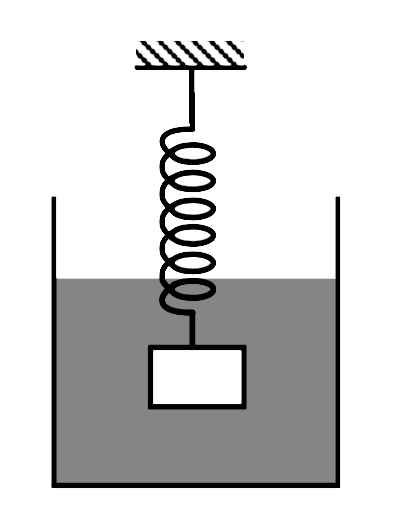 Aρ=ρ1x1−ρ2x2x1−x2Bρ=ρ1x2−ρ2x1x2−x1Cρ=ρ1x2+ρ2x1x2+x1Dρ=ρ1x2+ρ2x1x1+x2
Aρ=ρ1x1−ρ2x2x1−x2Bρ=ρ1x2−ρ2x1x2−x1Cρ=ρ1x2+ρ2x1x2+x1Dρ=ρ1x2+ρ2x1x1+x2 - Question 3 - Select One
If the time period (t) of vibration of a liquid drop depends on density (ρ) of the liquid, radius (r) of the drop and surface tension (S), then the expression of t is
where k is a dimensionless constant.At=k√ρr3SBsurface tensionCt=k√ρr3S1/2Dt=k√ρrS
A penguin floats first in a fluid of density ρ0 then in a fluid of density 0.95ρ0 and then in a fluid of density 1.1ρ0 . (a) Rank the densities according to the magnitude of the buoyant force on the penguin , greatest first . (b) Rank the densities according to the amount of fluid displaced by the penguin , greatest first.
View SolutionIf the time period (T)of vibration of a liquid drop depends on surface tension (S) , radius(r) of the drop , and density (ρ) of the liquid , then find the expression of T.
View SolutionWhat is the relationship between the buoyant force on an object and the liquid displaced by it?
View SolutionDerive an expression for the buoyant force acting on a body completely submerged in a liquid of density ρ.
View SolutionIf the time period (T)of vibration of a liquid drop depends on surface tension (S) , radius(r) of the drop , and density (ρ) of the liquid , then find the expression of T.
View Solution

