Two test tubes A and B of same mass with equal areas of cross-section are used as variable immersion hydrometer. If the length of test tube 'A' is double that of 'B', then the range of densities that can be measured by 'A' is
more than the range of densities that can be measured using 'B'.
less than the range of densities that can be measured wing 'B'.
equal to the range of densities that can be measured using 'B'.
Both (b) and (c).
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the length of the test tubes and the range of densities that can be measured by them.
1. Understanding the Concept of a Hydrometer:
A hydrometer measures the density of liquids. It works on the principle of buoyancy, where the amount of the hydrometer submerged in the liquid is inversely proportional to the density of the liquid.
2. Identifying the Given Information:
- Test tube A has a length that is double that of test tube B.
- Both test tubes have the same mass and equal areas of cross-section.
3. Analyzing the Effect of Length on Density Measurement:
- The range of densities that can be measured by a hydrometer is influenced by its length. A longer hydrometer can displace more liquid, allowing it to measure a wider range of densities.
- Since the length of test tube A is double that of test tube B, it can displace more liquid when immersed.
4. Determining the Range of Densities:
- If we denote the range of densities that can be measured by test tube B as RB, then the range of densities that can be measured by test tube A, denoted as RA, will be greater.
- Specifically, since the length of A is double that of B, the range of densities that can be measured by A will be double that of B. Thus, we can express this as:
RA=2×RB
5. Conclusion:
- Therefore, the range of densities that can be measured by test tube A is greater than that of test tube B.
Final Answer:
The range of densities that can be measured by test tube A is double that of test tube B.
A hydrometer measures the density of liquids. It works on the principle of buoyancy, where the amount of the hydrometer submerged in the liquid is inversely proportional to the density of the liquid.
- Test tube A has a length that is double that of test tube B.
- Both test tubes have the same mass and equal areas of cross-section.
- The range of densities that can be measured by a hydrometer is influenced by its length. A longer hydrometer can displace more liquid, allowing it to measure a wider range of densities.
- Since the length of test tube A is double that of test tube B, it can displace more liquid when immersed.
- If we denote the range of densities that can be measured by test tube B as RB, then the range of densities that can be measured by test tube A, denoted as RA, will be greater.
- Specifically, since the length of A is double that of B, the range of densities that can be measured by A will be double that of B. Thus, we can express this as:
RA=2×RB
- Therefore, the range of densities that can be measured by test tube A is greater than that of test tube B.
The range of densities that can be measured by test tube A is double that of test tube B.
Topper's Solved these Questions
- HYDROSTATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - CONCEPT APPLICATION (LEVEL 2)
20 Videos
- HYDROSTATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - CONCEPT APPLICATION (LEVEL 3)
10 Videos
- HYDROSTATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HYDROSTATICSEXERCISE - TEST YOUR CONCEPTS (ESSAY TYPE QUESTION)
4 Videos
- HEATBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HEATEXERCISE - CONCEPT APPLICATION Level 3
10 Videos
- KINEMATICS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICS EXERCISE - CONCEPT APPLICATION (Level 3) (Application Based Questions )
5 Videos
Similar Questions
Two strings A and B, made of the same material, have equal lengths. The cross sectional area of A is half that of B while the tension on A is twice that on B. The ratio of the velocities of transverse waves in A and B is:
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View Solution
Knowledge Check
Two test tubes A and B of same mass with equal areas of cross-section are used as variable immersion hydrometer. If the length of test 'A' is double that of 'B', then the range of densities that can be measured by 'A' is
Amore than the range of densities that can be measured using 'B'.Bless than the range of densities that can be measured using 'B'.Cequal to the range of densities that can be measured using 'B'.DBoth b and c.Two wires A and B are stretched by the same load. If the area of cross-section of wire 'A' is double that of 'B,' then the stress on 'B' is
Aequal to that on ABtwice that on AChalf that on ADfour times that on A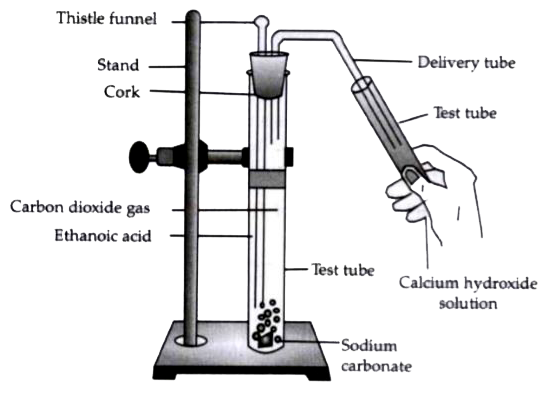
Name the gas released in test tube B.AOxygenBCarbon dioxideCHydrogenDNitrogen
Two metalic wires A and B are of same material and have equal length. If the cross-sectional area of B is double that of A, then which one among the following is the electrical resistance of B?
View SolutionTwo wires A and B have the same length and area of cross-section. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionA light rod of length L is suspended from a support horizonatlly by means of two vertical wires A and B of equal lengths as show in the figure . Cross-section area of A is half that of B and Young's modulus of A is double than that of B. A weight W is hung on the rod as shown. The value of x, so that the stress In A is same as that in B,is

View SolutionWhen a loaded test tube floats vertically with 13 and 14 of the lengths inside two liquids, then the ratio of the densities of the two liquids is
View SolutionBarn is used to measure the cross-sectional area of the mucles of an atom. IT is equal to
View Solution
