When a string fixed between two ends is plucked, a wave propagates along the string and reflects at the other end. Find the distance of maximum and minimum displacement of the particle in a wave from its first end, given that the velocity of wave propagation is and the frequency of vibration is 1320 Hz.
Distance of maximum diisplacement from one end
Distance of minimum displacement from one end = 0
Topper's Solved these Questions
Similar Questions
A tuning fork of frequency 250 Hz is vibrating at one end of a tube as shown in the figure. If maximum sound is heard at the other end, then the velocity of the waves will be
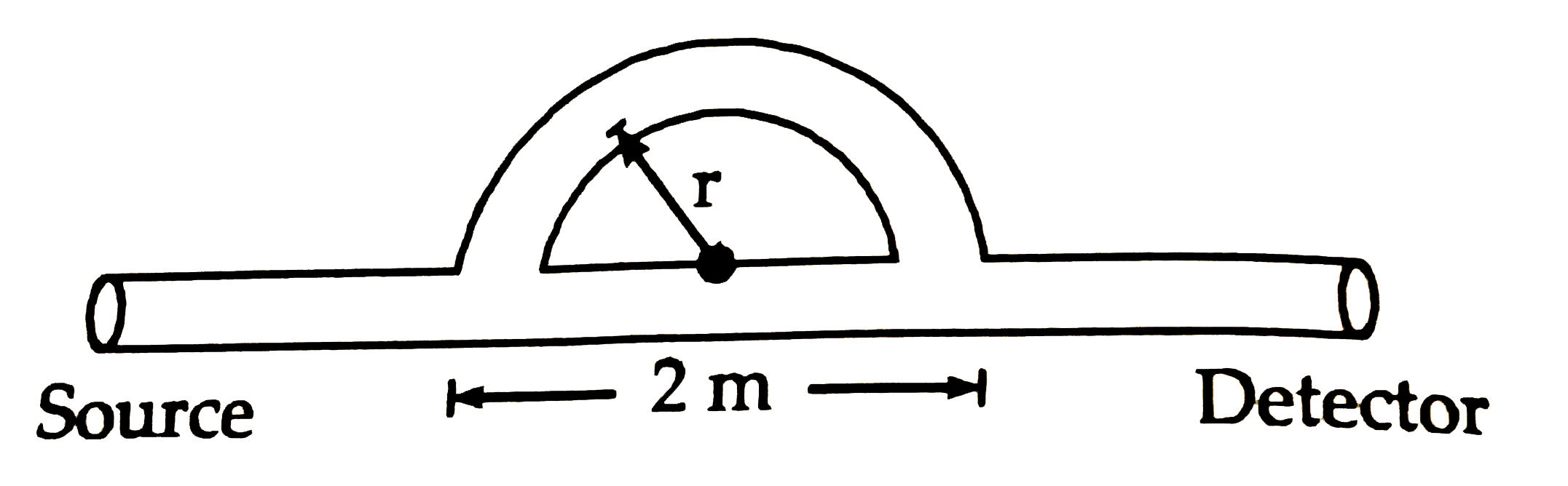
View SolutionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
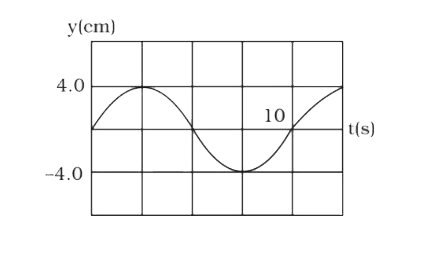
Q. The velocity of propagation of the wave is ?
View Solution
Knowledge Check
A string fixed at both ends oscillates in 5 segments, length 10 m and velocity of wave is 20 ms−1. What is the frequency?
A5 HzB15 HzC10 HzD2 HzDistance between nodes on a string is 5 cm. Velocity of transverse wave is 2ms−1. Then the frequency is
A5 HzB10 HzC20 HzD15 HzA pulse of a wave train travel s along a stretched string and reaches the fixed end of the string and reaches the fixed end of the string.it will be reflected back with
Aa phase change of 180∘ with velocity reversedBthe same phase as the incident pulse with no reversal of velocityCa phase change of 180∘ with no reveral of velocityDthe same phase as the incident pulse but with velocity reversed
A string fixed at both the ends forms standing waves with node separation of 5 cm. If the velocity of waves travelling in the string is 4 m/s, then the frequency of vibration of the string will be
View SolutionThe fundamental frequency of a stretched string fixed at both the ends is 50 Hz. If the velocity fo transverse wave created in string is 10ms−1 , find its length .
View SolutionA transverse sinusoidal wave of amplitude A, wavelength λ and frequency f is travelling along a stretch string. The maximum speed of any point on the string is v10, where, V is the velocity of wave propagation. If A=10−3m,andV=10ms−1, then λ and f are given by
View SolutionA wave on a stretched string is reflected from a fixed end P of the string. The phase difference, at P, between the incident and reflected waves is
View SolutionA string of length 2 m is fixed at both ends. If this string vibrates in its fourth normal mode with a frequency of 500 Hz then the waves wouldf travel on it is with a velocity of
View Solution
