Two iron spheres of equal mass having temperatures and are brought into contact with each other. What is the equilibrium temperature? Assume there is no heat loss to surroundings.
To find the equilibrium temperature when two iron spheres of equal mass at different temperatures are brought into contact, we can use the principle of conservation of energy. Here are the steps to solve the problem:
1. Identify the Initial Temperatures:
- Let the temperature of the first sphere (T1) be 20∘C.
- Let the temperature of the second sphere (T2) be 48∘C.
2. Assume Equal Mass:
- Let the mass of each sphere be m.
- Since both spheres are made of iron, we can assume they have the same specific heat capacity s.
3. Set Up the Heat Transfer Equation:
- When the two spheres are brought into contact, the heat lost by the hotter sphere will be equal to the heat gained by the cooler sphere.
- Heat lost by the second sphere (initially at 48∘C):
Qlost=m⋅s⋅(T2−Tf)=m⋅s⋅(48−Tf)
- Heat gained by the first sphere (initially at 20∘C):
Qgained=m⋅s⋅(Tf−T1)=m⋅s⋅(Tf−20)
4. Set the Heat Lost Equal to Heat Gained:
m⋅s⋅(48−Tf)=m⋅s⋅(Tf−20)
Since m and s are the same for both spheres, they can be canceled out:
48−Tf=Tf−20
5. Solve for the Final Temperature Tf:
- Rearranging the equation gives:
48+20=2Tf
68=2Tf
Tf=682=34∘C
6. Conclusion:
- The equilibrium temperature when the two iron spheres are brought into contact is 34∘C.
- Let the temperature of the first sphere (T1) be 20∘C.
- Let the temperature of the second sphere (T2) be 48∘C.
- Let the mass of each sphere be m.
- Since both spheres are made of iron, we can assume they have the same specific heat capacity s.
- When the two spheres are brought into contact, the heat lost by the hotter sphere will be equal to the heat gained by the cooler sphere.
- Heat lost by the second sphere (initially at 48∘C):
Qlost=m⋅s⋅(T2−Tf)=m⋅s⋅(48−Tf)
- Heat gained by the first sphere (initially at 20∘C):
Qgained=m⋅s⋅(Tf−T1)=m⋅s⋅(Tf−20)
m⋅s⋅(48−Tf)=m⋅s⋅(Tf−20)
Since m and s are the same for both spheres, they can be canceled out:
48−Tf=Tf−20
- Rearranging the equation gives:
48+20=2Tf
68=2Tf
Tf=682=34∘C
- The equilibrium temperature when the two iron spheres are brought into contact is 34∘C.
Similar Questions
Two bolcks to the same metal having same mass and at temperature T1 and T2 respectively ,are brought in contact with each other and allowed to attain thermal equilibrium at constant pressure .The change in entropy ,ΔS for this process is :
View SolutionRamu took four indentical iron balls of temperature 36∘C,10∘C,20∘C and 32∘C .He kept them in physical (thermal) contact with one another .After some time he measured the equilibrium temperautre attained by these four balls .What is the value of the equilibrium temperature?
View Solution
Knowledge Check
Two identical metallic balls of temperature 20∘Cand80∘C are kept in contact with each other. Then the ratio of heat by one ball to heat gained by another ball.
A2:1B3:2C1:1D2:3When two bodies at different temperatures are placed in thermal contact with each other, heat flows from the body at higher temperature to the body at lower temperature until they both acquire the same temperature. Assuming that there is no loss of heat to the surroundings,
Athe heat gained by the hotter body will be equal to the heat lost by the colder bodyBthe heat gained by the hotter body will be less than the heat lost by the colder bodyCthe heat gained by the hotter body will be greater than the heat lost by the colder bodyDthe heat lost by the hotter body will be equal to the heat gained by the colder body.Three copper blocks of masses M1,M2andM3 kg respectively are brought into thermal contact till they each equilibrium. Before contact, they were at T1,T2,T3(T1>T2>T3). Assuming there is no heat loss to the surroundings, the equilibrium temperature T is (s is specific heat of copper)
AT=T1+T2+T33BT=M1T1+M2T2+M3T3M1+M2+M3CT=M1T1+M2T2+M3T33(M1+M2+M3)DT=M1T1s+M2T2s+M3T3sM1+M2+M3
Three metallic spheres A,B and C have their masses in the ratio 1:2:3, specific heat capacities in the ratio 6:3:4. When the initial temperature of the spheres are measrued in Celsius scale, the ratio of their temperature is found to be 1:2:3. Initially the two spheres A and B are brought into contact. when equilibrium temperature is attained, sphere B is brought into contact with 'C'. Determine the ratio of the final temperatures of A,B and C as measured in Celsius scale.
View SolutionThree metallic spheres A,B and C have their masses in the ratio 1:2:3, specific heat capacities in the ratio 6:3:4. When the initial temperature of the spheres are measrued in Celsius scale, the ratio of their temperature is found to be 1:2:3. Initially the two spheres A and B are brought into contact. when equilibrium temperature is attained, sphere B is brought into contact with 'C'. Determine the ratio of the final temperatures of A,B and C as measured in Celsius scale.
View SolutionA 100 g cube of aluminium is removed from a bath of boiling water and dropped in a bath of room temperature water (2.00 litres at 20.0∘C). What is the final temperature of the water assuming heat loss to the surroundings is negligible? The specific heat capacity of aluminium is 897 J/kg.∘C.
View SolutionA table top is made of aluminium and has a hole of diameter 2 cm. An iron sphere of diameter 2.004 m is resting on this hole. Below the hole, an insulated container has 2 kg of water in it. Everything is at ambient temperature of 25∘C. The table top along with the iron sphere is heated till the ball falls through the hole into the water. Find the equilibrium temperature of the ball and water system
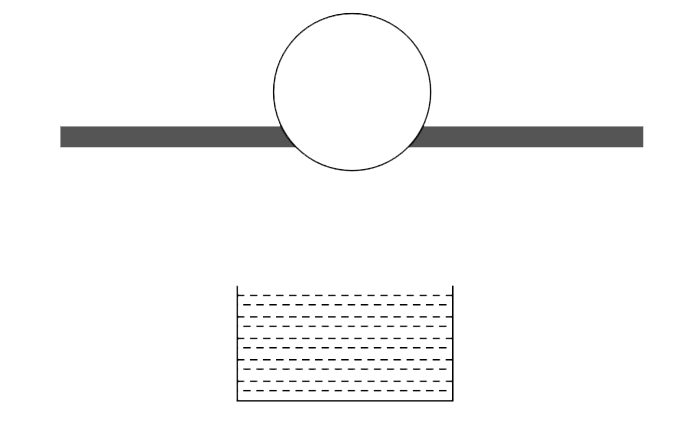
Neglect any heat loss from ball–water system to the surrounding and assume the heat capacity of the container to be negligible.
Relevant data: Coefficient of linear expansion for aluminium and iron are 2.4×10−5.∘C−1 and 1.2×10−5.∘C−1 respectively. Specific heat capacity of water and iron are 4200J.∘C−1g−1 and 450J.∘C−1g−1 respectively. Density of iron at 25∘C is 8000kg/m3.
View SolutionRamu took four indentical iron balls of temperature 36∘C,10∘C,20∘C and 32∘C .He kept them in physical (thermal) contact with one another .After some time he measured the equilibrium temperautre attained by these four balls .What is the value of the equilibrium temperature?
View Solution
