A thick metallic cylindrical rod which is to be cut when placed between th jasws of a 'vice' the handle to roated though 4×360∘, if the distance moved by the movable jaws is 0.5 cm per rotation then calculate the radius of the rod. (Assume that initially th jaws are in contact with each other)
2 cm
0.2 cm
1 cm
0.01 cm
The correct Answer is:C
From the question it is clear that the handle was rotated through .4. rotations (n).
∴ n =4 <br>Thedistancemovedbythemovab≤jawperrotation= 0.5 cm.<br> thereforeTotaldistancemovedbythejaw= 4 xx 0.5 cm =2cm.<br> therefore Thediameteroftherod=distancebetweenjawswhenrodisplacedbetweenthem.<br>d=2cm<br> rArr 2 r = 2 cm rArr r =1 cm <br> therefore Radius of the end =1 cm
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - OUR UNIVERSE EXERCISE - ASSESSMENT TEST (TEST 1)16videos
OUR UNIVERSE
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MOCK TESTEXERCISE - MULTIPLE CHOICE QUESTION25videos
MOCK TEST
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SOUNDEXERCISE - ASSESSMENT TESTS (TEST -2)14videos
SOUND
Similar Questions
A thick metallic cylindrical rod which is to be cut when placed between th jasws of a 'vice' the handle to roated though 4×360∘, if the distance moved by the movable jaws is 0.5 cm per rotation then calculate the radius of the rod. (Assume that initially th jaws are in contact with each other)
View SolutionA brass rod is 69.5 cm long and an aluminum rod is 49.0 cm long when both rods are at an initial temperature of 0∘C. The rods are placed in line with a gap of 1.5mm between them. The distance between the far ends of the rods remains same throughout. the temperapure is raised until the two rods are barely in contact. The coefficients of linear expansion of brass and aluminum are 2.0×10−5K−1 and 2.4×10−5K−1 respectively. In figure, the temperature at which contact of the rods barely occurs, in .∘C is closest to:
zView Solution
Knowledge Check
- Question 1 - Select One
A thick metallic cylindrical rod which is to be cut when placed between th jasws of a 'vice' the handle to roated though 4×360∘, if the distance moved by the movable jaws is 0.5 cm per rotation then calculate the radius of the rod. (Assume that initially th jaws are in contact with each other)
A2 cmB0.2 cmC1 cmD0.01 cm - Question 2 - Select One
The movable jaw of a vice moves through a distance of 7mm for one complete rotation of the handle. Through how many rotation shold the handle be rotated so that it holds a metal plate of thickness 3.5 cm firmly.
A3B5C312D212
The movable jaw of a vice moves through a distance of 7mm for one complete rotation of the handle. Through how many rotation shold the handle be rotated so that it holds a metal plate of thickness 3.5 cm firmly.
View SolutionThe movable jaw of a vice moves through a distance of 7mm for one complete rotation of the handle. Through how many rotation shold the handle be rotated so that it holds a metal plate of thickness 3.5 cm firmly.
View SolutionLeast count of a vernier callipers is 0.01cm When the two jaws of the instrument touch each other the 5th division of the vernier scale coincide with a main scale division and the zero of the vernier scale lies to the left of the zero of the main scale. Furthermore while measuring the diameter of a sphere, the zero markof the vernier scale lies between 2.4cm and 2.5cm and the 6th vernier division coincides with a main scale division. Calculate the diameter of the sphere.
View SolutionTwo balls of the same radius and weight are suspended on threads so that their surface are in contact. A charge of q0=4×10−7C is given to the balls which makes them repel each other and diverge to an angle of 60°. Find the mass of the balls if the distance of balls from the point of suspension to the centre of ball is 20cm. Find the density of the material of the balls if the angle of divergence becomes 54° when the balls are immersed in kerosene of density 800kgm−3 dielectric constant ofkerosene is εr=2[1.592g,255K/gm3]
View Solution(i) An organ pipe has one end closed and at the other end there is a vibrating diaphragm. The diaphragm is a pressure node. The pipe resonates when the frequency of the diaphragm is 2 KHz. Distance between adjacent nodes is 8.0 cm. When the frequency is slowly reduced, the pipe again resonates at 1.2 KHz.
(a) Find the length of the tube.
(b) Find the next frequency above 2 KHz at which the pipe resonates.
(ii) The figure shows an arrangement for measuring the speed of sound in air. A glass tube is fitted with a movable piston that allows the indicated length L to be adjusted. There is enough gap between the piston and the tube wall to allow the air to pass through it. A speaker is placed near the open end of the tube. A microphone is placed close to the speaker and it is connected to a waveform display. The display is a pure sinusoidal waveform making 750 oscillations in 5 s. Initially, the piston is held at end A and is then slowly pulled back. Loud sound is produced by the tube when L=50cm and L=157cm. Calculate the speed of sound in air.
 View Solution
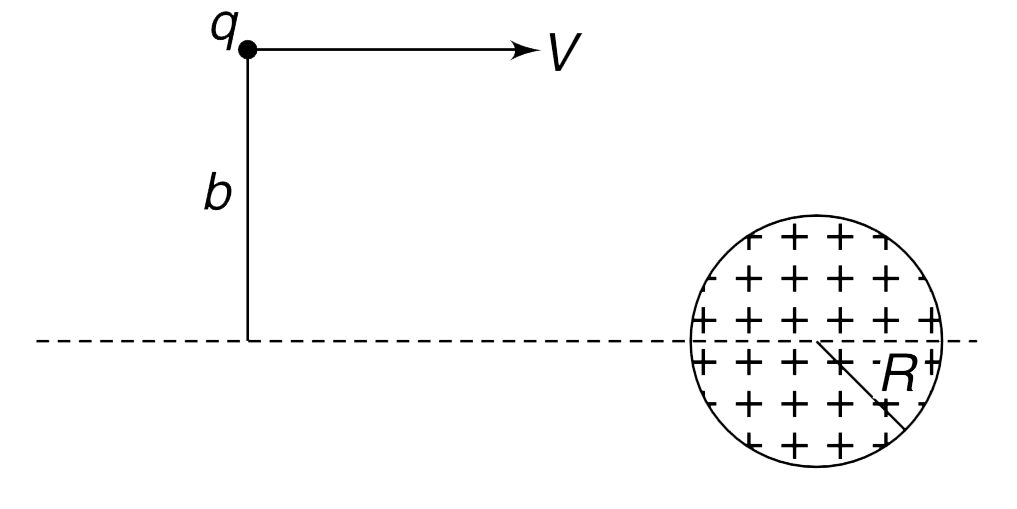
View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
 View Solution
View Solution

