
In the figure above ,AD=AC=BD. The point B, D and C are collinear. If ∠CAD=80∘, then find ∠DAB.
The correct Answer is:25∘
Step by step video, text & image solution for In the figure above ,AD=AC=BD. The point B, D and C are collinear. If angleCAD=80^(@), then find angleDAB. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure AD=BC,AC=BD. Then ΔPAB is
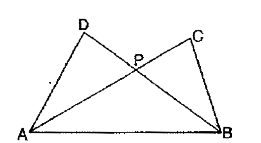 AequilateralBright angledCscaleneDisosceles
AequilateralBright angledCscaleneDisosceles - Question 2 - Select One
If the points (a,b),(c,d) and (a-c,b-d) are collinear, then
Aab=cdBac=bdCad=bcDNone
In Fig. AC and AD are tangent to a circle at C and D respectively. If ∠BCD=44∘, then find ∠CAD,∠ADC,∠CBD and ∠ACD.
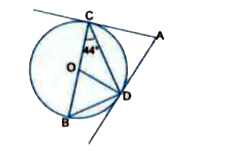 View Solution
View SolutionIn the figure,
AC=20, CB=15, AD=24.
Find AB and BD.
 View Solution
View SolutionIn the given figure if AC = 9, find BD.
 View Solution
View SolutionIn given figure AD = BC then AC and BD are equal or not?
 View Solution
View SolutionA cyclic quadrilateral ABCD is such that AB=BC,AD=DC and AC and BD intersect at O. If ∠CAD=46∘, then the measure of ∠AOB is equal to:
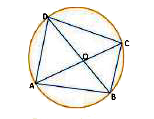 View Solution
View SolutionIn the figure, ¯¯¯¯¯¯DC || ¯¯¯¯¯¯AB. If ∠ACB=40∘ and ∠CAD=30∘, AC is the bisector of ∠DAB, then find the angle of ∠ADC.
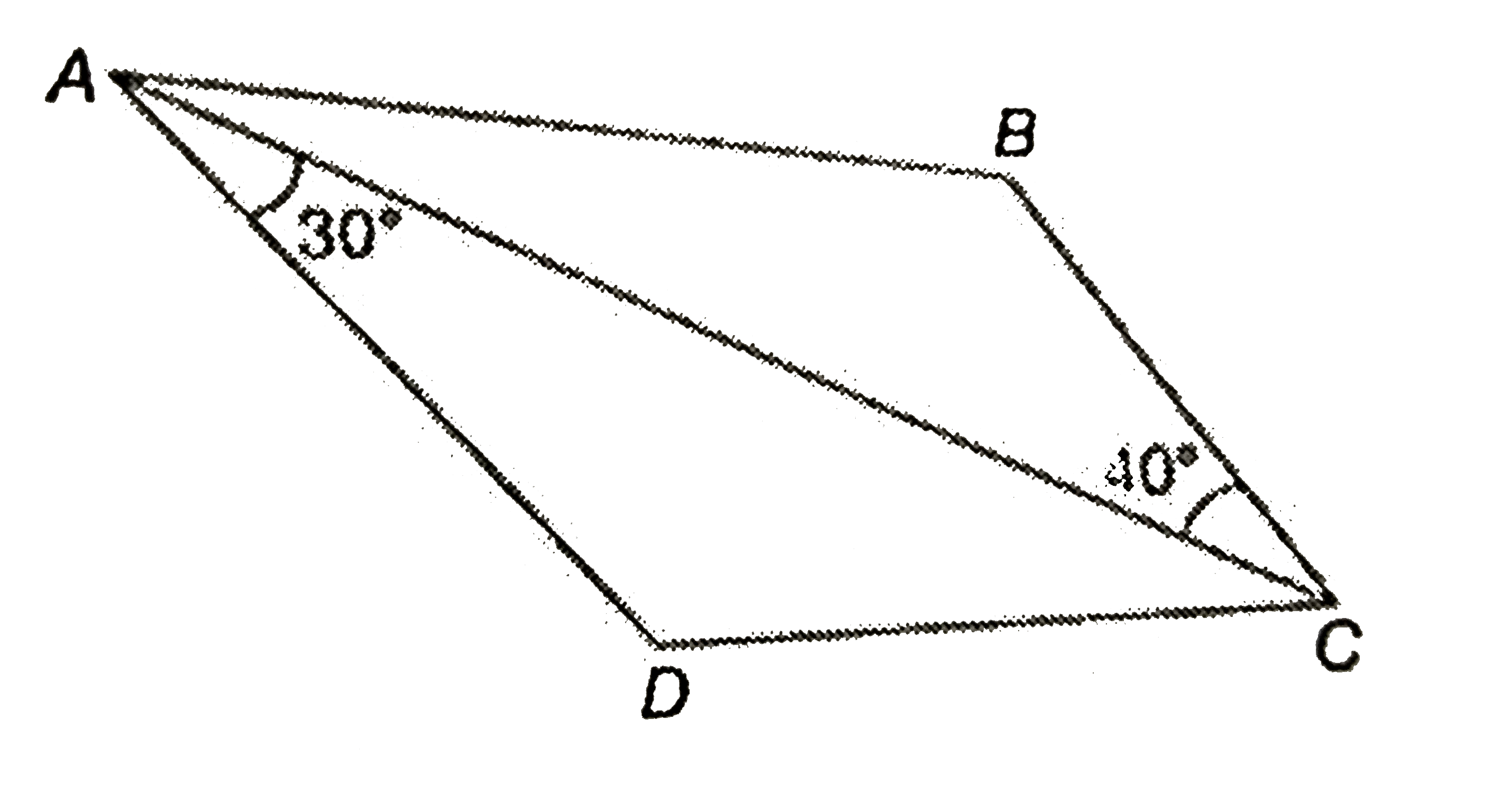 View Solution
View Solution


