The time taken by a man to row downstream is 35 the of the time taken by him to row upstream. If the product of the speeds of the man and the current is (both taken in kmph) 36, then find the speed of the man and the current .
12 kmph, 3 kmph
10 kmph, 2 kmph
9 kmph, 2 kmph
10 kmph, 3 kmph
The correct Answer is:A
To solve the problem step by step, we will define the variables, set up the equations based on the given information, and solve for the speeds of the man and the current.
1. Define Variables:
- Let the speed of the man be U km/h.
- Let the speed of the current be V km/h.
2. Establish Relationships:
- The speed of the man rowing upstream (against the current) is U−V.
- The speed of the man rowing downstream (with the current) is U+V.
3. Set Up Time Relationships:
- Let the distance rowed be D km.
- The time taken to row upstream is given by:
Tup=DU−V
- The time taken to row downstream is given by:
Tdown=DU+V
- According to the problem, the time taken to row downstream is 35 of the time taken to row upstream:
Tdown=35Tup
4. Substitute the Time Expressions:
DU+V=35⋅DU−V
- Since D is common on both sides, we can cancel it out (assuming D≠0):
1U+V=35⋅1U−V
5. Cross Multiply:
5=3⋅U+VU−V
- Rearranging gives:
5(U−V)=3(U+V)
6. Expand and Rearrange:
5U−5V=3U+3V
5U−3U=3V+5V
2U=8V
- Simplifying gives:
U=4V
7. Use the Product of Speeds:
- We know that the product of the speeds of the man and the current is given as:
U⋅V=36
- Substitute U=4V into the equation:
4V⋅V=36
4V2=36
V2=9
V=3 km/h
8. Find the Speed of the Man:
- Now substitute V back to find U:
U=4V=4⋅3=12 km/h
Final Answer:
- The speed of the man is 12 km/h.
- The speed of the current is 3 km/h.
- Let the speed of the man be U km/h.
- Let the speed of the current be V km/h.
- The speed of the man rowing upstream (against the current) is U−V.
- The speed of the man rowing downstream (with the current) is U+V.
- Let the distance rowed be D km.
- The time taken to row upstream is given by:
Tup=DU−V
- The time taken to row downstream is given by:
Tdown=DU+V
- According to the problem, the time taken to row downstream is 35 of the time taken to row upstream:
Tdown=35Tup
DU+V=35⋅DU−V
- Since D is common on both sides, we can cancel it out (assuming D≠0):
1U+V=35⋅1U−V
5=3⋅U+VU−V
- Rearranging gives:
5(U−V)=3(U+V)
5U−5V=3U+3V
5U−3U=3V+5V
2U=8V
- Simplifying gives:
U=4V
- We know that the product of the speeds of the man and the current is given as:
U⋅V=36
- Substitute U=4V into the equation:
4V⋅V=36
4V2=36
V2=9
V=3 km/h
- Now substitute V back to find U:
U=4V=4⋅3=12 km/h
- The speed of the man is 12 km/h.
- The speed of the current is 3 km/h.
Topper's Solved these Questions
- TIME AND DISTANCE BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - TIME AND DISTANCE EXERCISE - Concept Application (Level 1 )
30 Videos
- STATISTICS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - STATISTICS EXERCISE - CONCEPT APPLICATION (LEVEL II)
29 Videos
- TIME AND WORK PIPES AND CISTERNSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - TIME AND WORK PIPES AND CISTERNSEXERCISE - CONCEPT APPLICATION (LEVEL-3)
7 Videos
Similar Questions
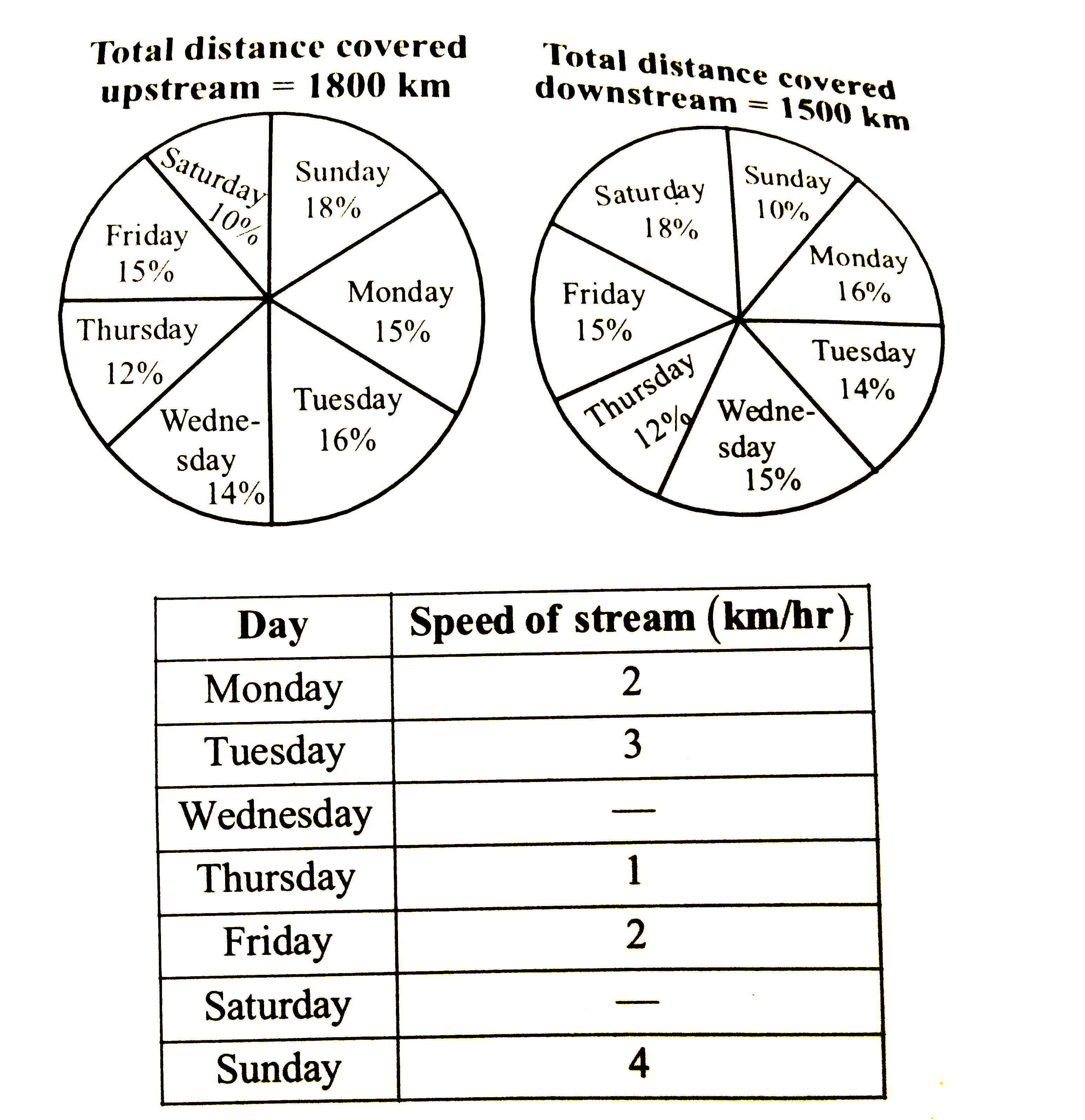
If the time taken by boat to travel upstream on Sunday is 2 hours more than the time takeb by it to travel downstream on Thursday and the speed of boat in still water on Thursday is 17 kmph, then find the upstream speed of boat on Sunday ?
View Solution
If the time taken by boat to travel upstream on Thursday is equla to the time taken by it to travel downstrem on Monday and the speed of boat in still water on Monday is 16 kmph then the speed in still water on Thursday?
View Solution
Knowledge Check
A man rows at the rate of 5 kmph in still water and his rate against the current is 3.5 kmph, then the man's rate along the current is:
A4.25 kmphB6 kmphC6.5 kmphD8.5 kmphA man rows a boat upstream a certain distance and then returns back to the same place. If the time taken by him in going upstream is twice the time taken in rowing downstream, find the ratio of the speed of the boat in still water and the speed of the stream.
A2:1B3:2C5:3D3:1A man rows at the rate of 5 kmph in still water and his rate against the current is 3.5 kmph, then the man's rate along the current is:
A8.5 km/hrB6.5 km/hrC6 km/hrD4.25 km/hr
A man car row - third of a kiometre downstream in 5 min and return to the starting point in another 10 min. Find the speed of the man in still water
View SolutionA man takes 20 minutes to row 12 km upstream which is a third more than the time he takes on his way downstream. What is his speed in still water?
View SolutionA man rows 10km upstream and the same distance downstream. The difference in time taken by the man in rowing upstream and downstream is 5min. If the speed of boat is 35km/hr, what is the speed of the stream?
View SolutionA man rows downstream 32 km and 14 km upstream, and he takes 6 hours to cover each distance. What is the speed of the current?
View SolutionA man can row 60 km downstream in 6 hours. If the speed of the current is 3 km/hr, then find in what time will he be able to cover 16 km upstream ?
View Solution
