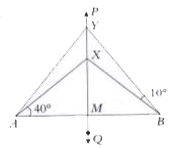
In the figuare above ( not to scale), ¯¯¯¯¯¯AD is the angle bisector of ∠EAF,∠AFC=110∘ and ∠DCF=20∘. If ∠DAF=30∘ and ∠EBD=10∘, then ∠AEB=
110∘
120∘
50∘
160∘
The correct Answer is:D
Step by step video, text & image solution for In the figuare above ( not to scale), bar(AD) is the angle bisector of /_EAF, /_AFC = 110^(@) and /_ DCF =20^(@). If /_ DAF =30^(@) and /_ EBD =10^(@), then /_ AEB = by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS (ESSAY TYPE QUESTIONS)
5 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check

In the figuare above ( not to scale), ¯¯¯¯¯¯AD is the angle bisector of ∠EAF,∠AFC=110∘ and ∠DCF=20∘. If ∠DAF=30∘ and ∠EBD=10∘, then ∠AEB=A110∘B120∘C50∘D160∘A monochromatic light source S of wavelength 440 nm is placed slightly above a plane mirror M as shown . Image of S in M can be used as a virtual source to produce interference fringes on the screen. The distance of source S from O is 20.0 cm, and the distance of screen from O is 100.0 cm (figure is not to scale). If the angle θ=0.50×10−3 radians, the width of the interference fringes observed on the screen is –
 A2.20 mmB2.64 mmC1.10 mmD0.55 mm
A2.20 mmB2.64 mmC1.10 mmD0.55 mm
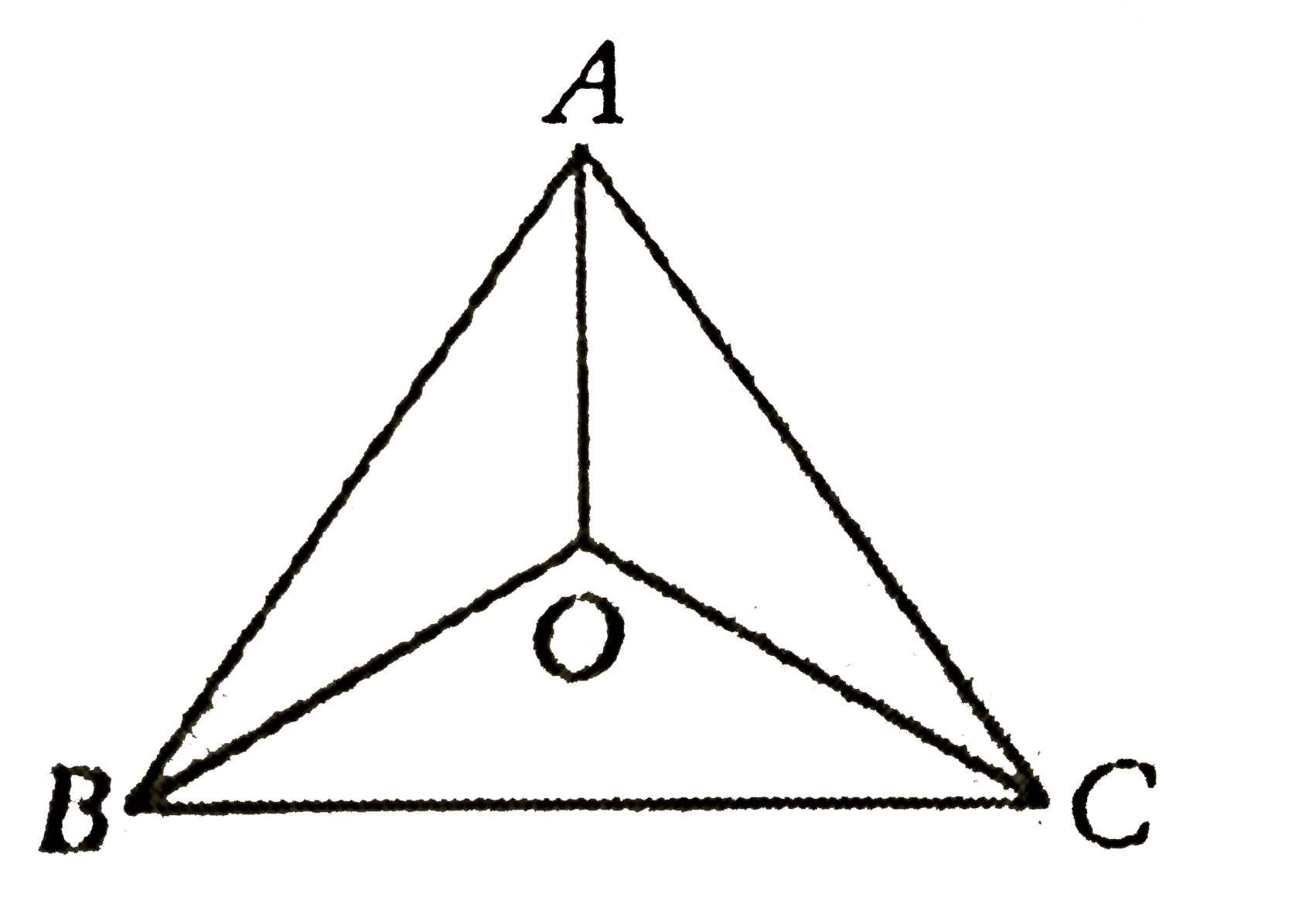
In the above ΔABC ( not to scale ), OA is the angle bisector of ∠BAC . If OB=OC,∠OAC=40∘ and ∠ABO=20∘. If ∠OCB=12∠ACO, then find ∠BOC.
View SolutionIn a ΔABC,∠A=120∘,AB=20cm,AC=30cm find the angle bisector AD .
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionIn the following figure, ¯¯¯¯¯¯BD is produced to E. If ¯¯¯¯¯¯AD is the angle bisector of ∠A, then find the ∠BCD.

View SolutionIn the following figure (not to scale), ∠DAB+∠CBA=90∘, BC = AD, AB = 20 cm, CD = 10 cm, then the area of the quadrilateral ABCD is:
निम्नलिखित आकृति (जो पैमाने के अनुसार नहीं है) में, ∠DAB+∠CBA=90∘, BC = AD, AB = 20 सेमी, CD = 10 सेमी है, तो चतुर्भुज ABCD का का क्षेत्रफल कितना होगा?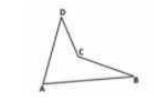
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists: List I (Time) List II (Angle between hour hand and and minute hand of a clock) A. 1.10 p.m. 1. 20o B. 2.15 p.m. 2. 2212o C. 8.40 p.m. 3. 24o 4. 25o 5. 30o A B C A B C (a) 4 2 1 (b) 4 3 2 (c) 5 2 1 (d) 4 3 2
View Solution